An object of mass m (in grams) attached to a coiled spring with damping factor b (in grams per second) is pulled down a distance a (in centimeters) from its rest position and then released. Assume that the positive direction of the motion is up and the period is T (in seconds) under simple harmonic motion. Develop a model that relates the distance d of the object from its rest position after t seconds.m = 30, a = 10, b = 0.55, T = 6
A. d = -10e-0.55t/60 cos 
B. d = -10e-0.55t/60 cos 
C. d = 10e0.55t/60 cos 
D. d = 10e-0.55t/60 cos 
Answer: B
You might also like to view...
Solve the problem.There are 1000 meters in 1 kilometer. Find a conversion factor between cubic meters and cubic kilometers. Write it in three forms.
A. 1 km2 = (1000 m)2 = 1,000 m2 B. 1 km3 = (1000 m)3 = 1,000,000,000 m3 C. 1 m3 = (1000 km)3 = 1,000,000 km3 D. 1 km3 = (1000 m)3 = 100,000 m3
Use implicit differentiation to find the specified derivative at the given point.Find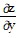 
at the point (9, 1, -1) for ln 
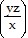- exy+z2 = 0.
A.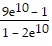 
B. 
C.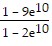 
D.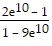 
Assign as indicated using the Huntington-Hill method.A hospital administrator wishes to assign ten emergency room medical teams to three outreach centers. The numbers of patients treated in an average week at the three centers are as follows:Center 1: 280 patientsCenter 2: 175 patientsCenter 3: 95 patientsHelp the administrator assign the medical teams to the three centers. Begin by giving each center one team.
A. Center 1: 5; Center 2: 3; Center 3: 2 B. Center 1: 5; Center 2: 4; Center 3: 1 C. Center 1: 4; Center 2: 4; Center 3: 2 D. Center 1: 4; Center 2: 3; Center 3: 3
Perform the indicated operation.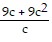
- 
A. -2(4c + 5) B. 2(5c + 5) C. (4c + 5) D. 2(4c + 5)