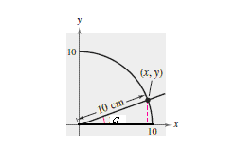
Use a compass to sketch a quarter of a circle of radius 10 centimeters. Using a protractor,
construct an angle of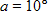 
in standard position (see figure). Drop a perpendicular line from the point of intersection of the terminal side of the angle and the arc of the circle. By actual measurement, calculate the coordinates 
of the point of intersection and use these measurements to approximate the six trigonometric functions of a 
angle. (Round your answer to two decimal places.)
?
?
A. sin10° ? 0.98, cos10° ? 0.17, tan10° ? 5.76,csc10° ? 0.18, sec10° ? 1.02, cot10° ? 5.67
B. sin10° ? 5.67, cos10° ? 1.02, tan10° ? 5.76,csc10° ? 0.18, sec10° ? 0.98, cot10° ? 5.67?
C. sin10° ? 0.17, cos10° ? 0.98, tan10° ? 0.18,csc10° ? 5.76, sec10° ? 1.02, cot10° ? 5.67?
D. sin10° ? 0.18, cos10° ? 0.98, tan10° ? 0.17,csc10° ? 10, sec10° ? 0.98, cot10° ? 5.76?
E. sin10° ? 0.17, cos10° ? 0.98, tan10° ? 0.18,csc10° ? 5.76, sec10° ? 5.67, cot10° ? 1.02
Answer: C
You might also like to view...
Solve for the specified variable.A =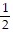 
bh for b
A. b =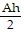 
B. b =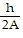 
C. b =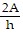 
D. b =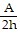 
Solve the inequality. Write the solution set in interval notation and graph it.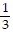
(15x + 33) + 
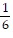(18x - 36) > 69
A.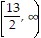 
B. [8, ?)
C.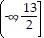 
D. (-?, 8]
Solve.The total sales in dollars of some small businesses fluctuates according to the equation 
where x is the time in months, with x = 1 corresponding to January,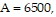 
and 
Determine the month with the greatest total sales and give the sales in that month.
A. March; $10,300 B. June; $6500 C. December; $10,300 D. September; $2700
Solve the system of equations.
A. x = 3z + 1, and y = z - 3, where z is any real number or {(x, y, z) |x = 3z + 1, and y = z - 3, where z is any real number} B. x = -3 - z, and y = 3z + 1, where z is any real number or {(x, y, z) |x = -3 - z, and y = 3z + 1, where z is any real number} C. x = z + 3, and y = 3z + 1, where z is any real number or {(x, y, z) |x = z + 3, and y = 3z + 1, where z is any real number} D. inconsistent