A gas-fired industrial furnace is used to generate steam. The furnace is a 3 m cubic structure and the interior surfaces are completely covered with boiler tubes transporting pressurized wet steam at 150°C. It is desired to keep the furnace losses to 1% of the total heat input of 1 MW. The outside of the furnace can be insulated with a blanket-type mineral wool insulation [k = 0.13 W/(m °C)], which is protected by a polished metal sheet outer shell. Assume the floor of the furnace is insulated. What is the temperature of the metal shell sides? What thickness of insulation is required?
GIVEN
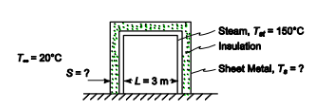
? An insulated cubic furnace with steam filled tubes on the inner walls
? Steam temperature (Tst) = 150°C
? Length of a side of the furnace (L) = 3 m
? Thermal conductivity of mineral wool insulation (ki) = 0.13 W/(m°C)
? Insulation is protected by metal sheet outer shell
? Furnace losses (qc) = 1% of total heat input
? Total heat input (qin) = 1 MW = 106 W
FIND
(a) Temperature of the metal sheel sides (Ts)
(b) The thickness of insulation (s) required
ASSUMPTIONS
? Steady state operation
? Thermal resistance of the convection within the steam pipes, the steam pipe walls, the furnace
walls, and the metal shell negligible compared to that of the insulation
? Air outside the furnace is still
? The floor is well insulated —heat loss is negligible
? Temperature of the metal shell is uniform
? Ambient temperature (T?) = 20°C (293 K)
? Edge effects are negligible
? The emissivity of the polished metal shell (E) = 0.05 (see Table 9.2)
SKETCH
PROPERTIES AND CONSTANTS
From Appendix 1, Table 5, the Stephan-Boltzmann Constant
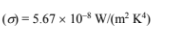
(a) Since the Grashof number on the outside of the metal shell will depend on the temperature of the metal shell, an iterative procedure is required. For the first iteration, let Ts = 100°C (373 K).
From Appendix 2, Table 28, for dry air at the mean temperature of 60°C
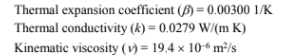
The Grashof number for the four sides of the furnace, assuming the insulation thickness is small compared to 3 m, is
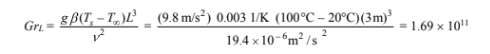
The heat transfer from the furnace will be calculated by treating the sides as vertical flat plates and the top as a horizontal flat plate facing upward. From Equation (8.13), the heat transfer coefficient for the sides is

The characteristic dimension for the top of the furnace (Lc) is
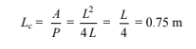
The Grashof and Rayleigh numbers based on this dimension are
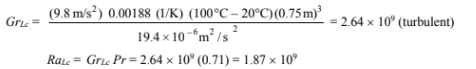
The average Nusselt number is given by Equation (8.16)
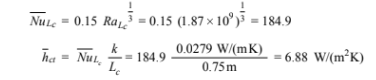
The rate of convection and radiation must be 1% of the total heat input
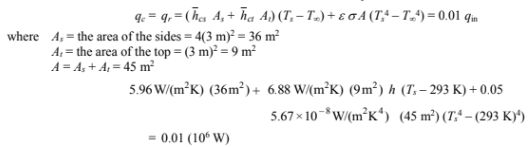
By trial and error: Ts = 327 K = 54°C
Following the same procedure for other iterations
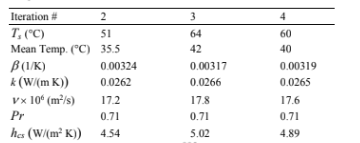
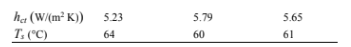
Therefore, the surface temperature (Ts) ? 61°C
(b) The rate of conductive heat transfer through the insulation must also be 1% of the input heat
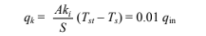
Solving for the insulation thickness
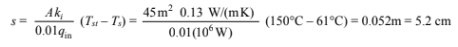
You might also like to view...
The _____ of an object is a measure of the amount of matter in the object
A) weight B) mass C) height D) velocity
A circular loop of wire has its radius reduced in half in time ?t. A uniform magnetic field is at an angle of 60° to the plane of the coil, and the magnetic field doubles its intensity in the same time interval ?t. During this interval, what happens to the flux through the coil?
a. It increases. b. It decreases. c. It remains the same. d. More information is needed to make this conclusion.
Which of the following wavelength regions can be studied with telescopes on the ground?
A) radio, visible, and very limited portions of the infrared and ultraviolet regions B) all light with wavelengths longer than ultraviolet wavelengths C) all light with wavelengths shorter than infrared wavelengths D) infrared, visible, and ultraviolet light
When the principal quantum number is n = 5, how many different values of ? are possible?
1.1 2.5 3.9 4.25