Decide whether or not the points are the vertices of a right triangle.Consider the three points A = (7, 7), B = (9, 11), C = (11, 10). Determine whether the triangle ABC is a right triangle. Explain your reasoning.
A. The side lengths of triangle ABC are d(A, B) = 3
, d(A, C) = 5, d(B, C) = 
.
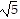[d(A, B)]2 + [d(B, C)]2 = (3
)2 + (
)2 = 18 + 5 = 23
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
B. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 5, d(B, C) = 
.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + (
)2 = 20 + 5 = 25
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
C. The side lengths of triangle ABC are d(A, B) = 2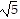
, d(A, C) = 2
, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2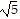
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = (2
)2 = 24
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
D. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 5, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
Answer: B
You might also like to view...
Evaluate the integral using the given substitution.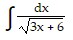
, u = 3x + 6
A. 2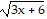
+ C
B. 
+ C
C. 
+ C
D. 
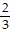
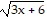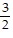
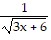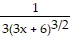+ C
Find the domain of the given function.f(x) =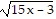 
A. all real numbers x where x ? -3
B. all real numbers x where x ?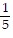 
C. all real numbers x where x > 3
D. all real numbers x where x > -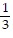 
Find the set if the universal set U = {-8, -3, -1, 0, 2, 4, 5, 6, 7, 9}, A = {-8, -3, -1, 2, 5}, B = {-3, 2, 5, 7}, and C = {-1, 4, 9}.(A ? C)'
A. {-8, -3, 0, 2, 4, 5, 6, 7, 9} B. {-8, -3, -1, 2, 4, 5, 7, 9} C. {-1} D. {-8, -3, -1, 2, 4, 5, 6, 7, 9}
Simplify.8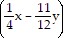
A. 8x -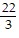 
y
B. 2x - 
y
C. 2x - 
y
D. 2x - 
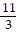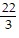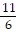y