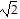Solve the problem.Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 1.3 feet per second. Find a function, d(t), which gives the distance Ken is from the streetlight in terms of time. Find a function,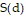 
, which gives the length of Ken's shadow in terms of d. Then find 
.
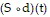A. (S ? d)(t) = 0.72t
B. (S ? d)(t) = 1.24t
C. (S ? d)(t) = 2.2t
D. (S ? d)(t) = 0.98t
Answer: D
You might also like to view...
Find the area under the curve of the function on the stated interval. Do so by dividing the interval into n equal subintervals and finding the area of the corresponding circumscribed polygon.f(x) = 2x2 + x + 3 from x = -2 to x = 1; n = 6
A. 7 B. 13 C. 11 D. 9
Find the expected value.You are given 5 to 1 odds against tossing 2 tails in 2 tosses of a fair coin. This means that you win $5 if you succeed and you lose $1 if you fail. Find the expected value (to you) of the game. Round to the nearest cent.
A. $0.75 B. -$0.50 C. $1.25 D. $0.50
Complete the income statement. Frank's Nursery had gross sales of $2,273,000 with returns of $57,800. The inventory on January 1 was $567,000. During the year $1,130,000 worth of goods was purchased with freight of $5,600. The inventory on December 31 was $525,000. Wages and salaries were $81,600, rent was $10,200, advertising was $17,700, utilities were $5,200, business taxes totaled $8,500, and miscellaneous expenses were $6,100.
A. 1) $2,273,000, 2) $57,800, 3) $2,215,200, 4) $1,177,600, 5) $1,037,600,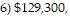 
B. 1) $2,273,000, 2) $57,800, 3) $2,215,200, 4) $1,166,400, 5) $1,048,800,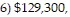 
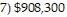
C. 1) $2,273,000, 2) $57,800, 3) $2,215,200, 4) $1,177,600, 5) $1,037,600,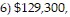 
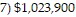
D. 1) $2,273,000, 2) $57,800, 3) $2,330,800, 4) $1,177,600, 5) $1,153,200,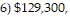 
Write the expression in standard form.9 +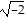 
+ 7 -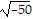 
A. 16 - 4i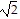
B. 16 + 4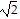
C. 16 - 4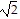
D. 16 + 4i