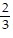Solve the problem.Ron throws a ball straight up with an initial speed of 70 feet per second from a height of 7 feet. Find parametric equations that describe the motion of the ball as a function of time. How long is the ball in the air? When is the ball at its maximum height? What is the maximum height of the ball?
A. x = 0, y = -16t2 + 70t + 7
8.545 sec, 2.188 sec,
591.246 feet
B. x = 0, y = -16t2 + 70t + 7
4.273 sec, 2.188 sec,
6.974 feet
C. x = 0, y = -16t2 + 70t + 7
4.473 sec, 2.188 sec,
83.563 feet
D. x = 0, y = -16t2 + 70t + 7
8.946 sec, 2.188 sec,
76.563 feet
Answer: C
You might also like to view...
Give an appropriate answer.If f(x, y, z) = (x4 + y2 + z)2 find fyy(x, y, z).
A. 4x4 + 12y2 + 4z B. 8y2(x4 + y2 + z) C. 4y2(x4 + y2 + z) D. 2x4 + 6y2 + 2z
Suppose that f satisfies the equation of change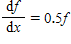 
. The initial value of f is 2.9. Make a graph of f. Use a horizontal span of 0 to 5.
What will be an ideal response?
Solve the problem.An office contains 1000 ft3 of air initially free of carbon monoxide. Starting at time = 0, cigarette smoke containing 4% carbon monoxide is blown into the room at the rate of 0.5 ft3/min. A ceiling fan keeps the air in the room well circulated and the air leaves the room at the same rate of 0.5ft3/min. Find the time when the concentration of carbon monoxide reaches 0.01%.
A. 6.01 min B. 5.01 min C. 7.01 min D. 8.01 min
Use the given zero to find the remaining zeros of the function.f(x) = 3x4 - 29x3 + 111x2 - 179x + 78; zero: 3 + 2i
A. 3 - 2i, 3,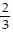 
B. 2 - 3i, -3, -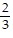 
C. 3 - 2i, -3,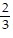 
D. 2 - 3i, 3, - 