Solve the problem.The linear function f computes the distance y in miles between a car and the city of Quebec after x hours, where 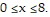 The graphs of f and the horizontal lines
The graphs of f and the horizontal lines 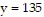 and
and 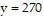 are shown in the figure. (i) Is the car moving toward or away from Quebec? (ii) Determine the times when the car is 135 miles and 270 miles from Quebec.
are shown in the figure. (i) Is the car moving toward or away from Quebec? (ii) Determine the times when the car is 135 miles and 270 miles from Quebec. 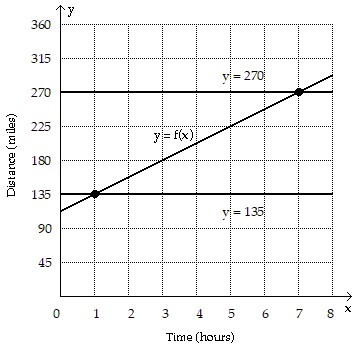
A. away from Quebec.; The car is 135 miles from Quebec after 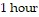 and
and 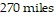 after
after 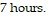
B. away from Quebec.; The car is 135 miles from Quebec after 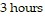 and
and 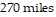 after
after 
C. away from Quebec.; The car is 135 miles from Quebec after 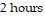 and
and 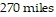 after
after 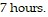
D. toward from Quebec.; The car is 135 miles from Quebec after 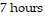 and
and 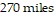 after
after 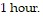
Answer: A
You might also like to view...
Multiply.-3.82 ? (-5.5)
A. 9.32 B. -1.68 C. 21.01 D. -9.32
Translate the description to symbolic form.The surface area for a sphere is four times the product of ? and the square of the radius.
A. 16?r2 B. 4?2r2 C. 4?r2 D. 4?r
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.(x + 3)2 - 16(y - 4)2 = 16
A. center at (-3, 4)
transverse axis is parallel to y-axis
vertices at (-3, 0) and (-3, 8),
foci at (-3, 4 -  ) and (-3, 4 +
) and (-3, 4 +  ),
),
asymptotes of y + 4 = - 4(x - 3) and y + 4 = 4(x - 3)
B. center at (-3, 4)
transverse axis is parallel to x-axis
vertices at (-7, 4) and (1, 4)
foci at (-3 - 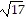 , 4) and (-3 +
, 4) and (-3 + 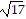 , 4)
, 4)
asymptotes of y - 4 = - 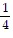 (x + 3) and y - 4 =
(x + 3) and y - 4 = 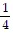 (x + 3)
(x + 3)
C. center at (4, -3)
transverse axis is parallel to x-axis
vertices at (0, -3) and (8, -3)
foci at (4 - 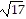 , -3) and (4 +
, -3) and (4 + 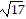 , -3)
, -3)
asymptotes of y + 3 = -  (x - 4) and y + 3 =
(x - 4) and y + 3 =  (x - 4)
(x - 4)
D. center at (-3, 4)
transverse axis is parallel to x-axis
vertices at (-4, 4) and (-2, 4)
foci at (-3 - 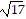 , 4) and (-3 +
, 4) and (-3 + 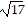 , 4)
, 4)
asymptotes of y - 4 = - 4(x + 3) and y - 4 = 4(x + 3)
Evaluate using a table of integration formulas.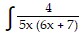 dx
dx
A. 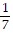 ln
ln 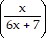 + C
+ C
B. 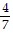 ln
ln 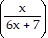 + C
+ C
C. 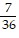 +
+ 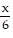 -
- 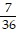 ln (6x + 7) + C
ln (6x + 7) + C
D. 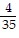 ln
ln 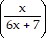 + C
+ C