Find the location of the indicated absolute extrema for the function.Maximum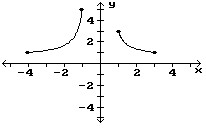
A. (-1, 5)
B. (1, 3)
C. None
D. (3, 1)
Answer: A
You might also like to view...
Solve.The orbit of a planet around a sun is an ellipse with the sun at one focus. The aphelion of a planet is its greatest distance from the sun, its perihelion is its shortest distance, and its mean distance is the length of the semimajor axis of the elliptical orbit. If a planet has a perihelion of 455.7 million miles and a mean distance of 458 million miles, write an equation for the orbit of the planet around the sun.
A. 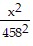 +
+ 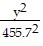 = 1
= 1
B. 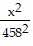 +
+ 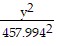 = 1
= 1
C. 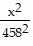 +
+ 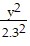 = 1
= 1
D. 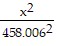 +
+  = 1
= 1
Sketch the indicated set. Describe the boundary of the set. Finally, state whether the set is open, closed or neither.D = {(x, y) : 2 < 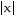 +
+ 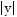 < 4}
< 4}
A. 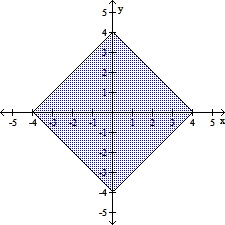
The boundary is the square with vertices
(-4, 0), (0, 4), (4, 0), and (0, -4). The interior
is the set of all points in the region inside
the boundary square. The set is open.
B. 
The boundary is the square with vertices
(-2, 0), (0, 2), (2, 0), and (0, -2). The interior
is the set of all points inside the boundary
square. The set is open.
C. 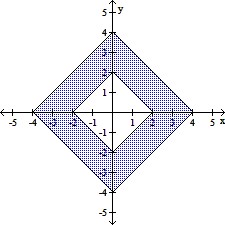
The boundaries are squares. The first has
vertices (-2, 0), (0, 2), (2, 0), and (0, -2)
and the second has vertices (-4, 0), (0, 4),
(4, 0), and (0, -4). The set is open.
D. 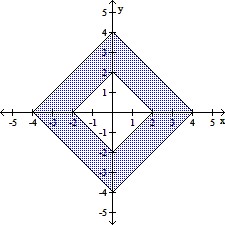
The boundaries are squares. The first has
vertices (-2, 0), (0, 2), (2, 0), and (0, -2)
and the second has vertices (-4, 0), (0, 4),
(4, 0), and (0, -4). The set is closed.
Find the quotient using long division.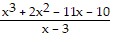
A. x2 - x - 12 + 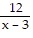
B. x2 + 5x + 4 + 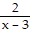
C. x2 - 5x - 4 + 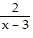
D. x2 - 5x + 4 - 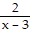
Use the graph to find the intervals on which it is increasing, decreasing, or constant.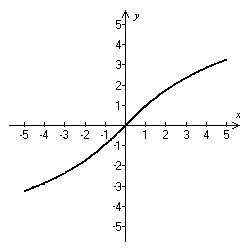
A. Increasing on (-?, ?) B. Increasing on (-?, 0); decreasing on (0, ?) C. Decreasing on (-?, ?) D. Decreasing on (-?, 0); increasing on (0, ?)