Find the zeros of the polynomial function. State whether the graph crosses the x-axis, or touches the x-axis and turns around, at each intercept. f(x) = -x2(x + 4)(x2 - 1)
A. x = 0, touches the x-axis and turns around;
x = -4, crosses the x-axis;
x = 1, touches the x-axis and turns around
B. x = 0, crosses the x-axis;
x = -4, crosses the x-axis;
x = -1, crosses the x-axis;
x = 1, crosses the x-axis
C. x = 0, touches the x-axis and turns around;
x = -4, crosses the x-axis;
x = -1, crosses the x-axis;
x = 1, crosses the x-axis
D. x = 0, touches the x-axis and turns around;
x = 4, crosses the x-axis;
x = -1, touches the x-axis and turns around;
x = 1, touches the x-axis and turns around
Answer: C
You might also like to view...
Solve the problem.The position of a particle moving along a coordinate line is s =  , with s in meters and t in seconds. Find the particle's velocity at
, with s in meters and t in seconds. Find the particle's velocity at 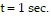
A. 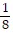 m/sec
m/sec
B. 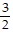 m/sec
m/sec
C. 3 m/sec
D. - 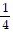 m/sec
m/sec
Solve the inequality. Write the solution set in interval notation and graph it.6 < 3x ? 21 ![]()
A. (-2, 1]![]()
B. [-2, 1)![]()
C. (2, 7]![]()
D. [2, 7)![]()
Find the real zeros, if any, of each quadratic function using the quadratic formula. List the x-intercepts, if any, of the graph of the function. f(x) = 4x2 - 25x - 21
A. x = - 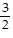 , x = 14
, x = 14
B. x = - 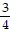 , x = 7
, x = 7
C. x = -3, x = 7
D. x =  , x = -7
, x = -7
Write the first five terms of the sequence defined recursively. Use the pattern to write the nth term of the sequence as a function of n.
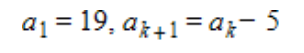
a. 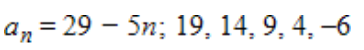
b. 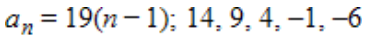
c. 
d. 