Design a heat pipe cooling system for a spherical satellite that dissipates 5000 W/m3 , has a surface area of 5 m2 , and cannot exceed a temperature of 120°C. All the heat must be dissipated by radiation into space. State all your assumptions.
GIVEN

FIND
(a) A design for a heat pipe cooling system
ASSUMPTIONS
? Temperature drop between the satellite interior and the heat pipe evaporator is < 20°C
? Neglect vapor pressure drop in the heat pipe
Since the satellite has a 5 m2 surface area, the radius of the spherical satellite is
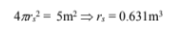
from which the satellite volume is
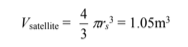
and the total power dissipated by the satellite, and therefore by the heat pipe cooling system, is
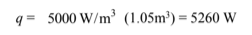
Since we have assumed that the temperature drop between the satellite interior and the heat pipe evaporator is less than 20°C, we can safely operate the heat pipe at 100°C.
From Figure 9.24, water has the highest figure of merit, M, at the desired temperature of 373 K and it should operate satisfactorily at the desired temperature. From that figure we find
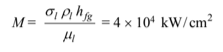
Since we have neglected vapor neglected vapor pressure drop, and since there is no gravitational head, Equation (9.40) simplifies to
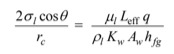
Rearranging the previous equation to solve for the geometry of the heat pipe
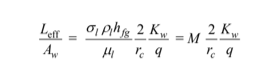

For a reasonably sized heat pipe, let Leff = 30 cm. Then the total wick cross-sectional area required is Aw = 30 cm/ 2.4 cm–1 = 12.5 cm2. Assuming that we need N pipe of diameter D and thickness t, we have
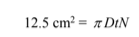
If the exterior surface of the heat pipe condenser section is black, the following equation gives the required surface area of the condenser section
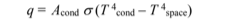
This equation assumes that the heat pipes are separated sufficiently that they all have a near-unity shape factor with respect to space.
Using Tcond = 100°C = 373 K and assuming Tspace = 0 K and we can solve for the condenser surface area as follows
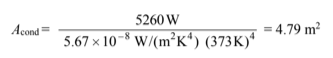
If the condenser length is Lcond, then
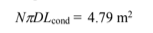
Let Lcond = 10 cm giving N?D = 47.9 m = 4790 cm. Since we found previously that ?DtN = 12.5 cm2, we can solve for the wick thickness t
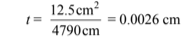
Choose a pipe diameter of 3 cm, then
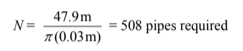
Since Leff = L + (Lcond + Levap)/2, letting the evaporator and condenser lengths be the same, 10 cm, we
find L = 20 cm and the overall length is 20 + 10 + 10 = 40 cm. We summarize the cooling system below
Pipe diameter = 3 cm
Pipe length = 40 cm
Condenser length = 10 cm
Evaporator length = 10 cm
Adiabatic section length = 20 cm
Wick: 0.0026 cm thickness of 200 mesh nickel powder
Working fluid: water
Pressure: atmospheric
Number of pipes required: 508
You might also like to view...
Animated and interactive elements might require that your visitors install ______ to allow the element to play in the visitors' browser.
A. scripts B. add-ons C. operating systems D. plug-ins
Which term in the simplified Drake equations depends on sociological factors?
A) NHP B) flife C) fciv D) fnow
When light shines on a lens placed on a flat piece of glass, interference occurs which causes circular fringes called Newton's rings. The two beams that are interfering come:
a. from the top and bottom surface of the lens. b. from the top surface of the lens and the top surface of the piece of glass. c. from the bottom surface of the lens and the top surface of the piece of glass. d. from the top and bottom surface of the flat piece of glass.
The photons of blue light have:
A) more energy than the photons of red light. B) more energy than the photons of ultraviolet light. C) a lower frequency than the photons of red light. D) a longer wavelength than the photons of red light.