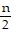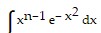Solve the problem.An object is propelled vertically upward from the top of a 304-foot building. The quadratic function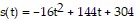 
models the ball's height above the ground, 
in feet, t seconds after it was thrown. How many seconds does it take until the object finally hits the ground? Round to the nearest tenth of a second if necessary.
A. 2 seconds
B. 10.8 seconds
C. 1.8 seconds
D. 4.5 seconds
Answer: B
You might also like to view...
Find the extreme values of the function subject to the given constraint.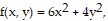
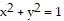
A. Minimum: 4 at (0, ±1); maximum: 0 at (0, 0) B. Minimum: 4 at (0, ±1); maximum: 6 at (±1, 0) C. Minimum: 4 at (±1, 0); maximum: 0 at (0, 0) D. Minimum: 4 at (±1, 0); maximum: 6 at (0, ±1)
Translate to an equation and solve.2.1 is what percent of 4?
A. 57.5% B. 50.5% C. 53.5% D. 52.5%
Calculate the instantaneous velocity for the given value of t of an object moving with rectilinear motion according to the given function relating s (in ft) and t (in s)s =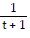 
; t = 3
A. - 
ft/s
B. 
ft/s
C. 
ft/s
D. - 
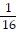ft/s
Use integration by parts to establish a reduction formula for the integral.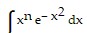
A.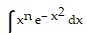 
= - 
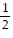xn-1 e- x2 +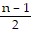 
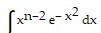
B.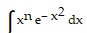 
= n xn-1 e- x2 + 2n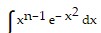 
C.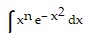 
= - 2xn-1 e- x2 - 2(n - 1)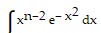 
D.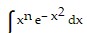 
= - 
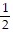xn e- x2 + 
