Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. Determine where the function is increasing and where it is decreasing. If necessary, round answers to two decimal places.f(x) = 0.15x4 + 0.3x3 - 0.8x2 + 5; (-4, 2)
A. local maximum at (0, 5)
local minima at (-2.55, 1.17) and (1.05, 4.65)
increasing on [-2.55, 0] and [1.05, 2]
decreasing on [-4, -2.55] and [0, 1.05]
B. local maximum at (0, 5)
local minima at (-2.55, 1.17) and (1.05, 4.65)
increasing on [-4, -2.55] and [0, 1.05]
decreasing on [-2.55, 0] and [1.05, 2]
C. local maximum at (-2.55, 1.17) and (1.05, 4.65)
local minima at (0, 5)
increasing on [-4, -2.55] and [0, 1.05]
decreasing on [-2.55, 0] and [1.05, 2]
D. local maximum at (-2.55, 1.17) and (1.05, 4.65)
local minima at (0, 5)
increasing on [-2.55, 0] and [1.05, 2]
decreasing on [-4, -2.55] and [0, 1.05]
Answer: A
You might also like to view...
Find the least common denominator.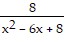 +
+ 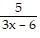
A. 3(x - 4)(x - 2) B. 3(x + 4)(x + 2) C. 3(x + 4)(x - 2) D. 3(x - 4)(x + 2)
Solve the problem.The profit function for a product is given by P(x) = -0.7x3 + 115.5x2 - 3710x - 84,000 dollars, where x is the number of units produced and sold. Determine the levels of production and sale that give break-even.
A. 80 or 100 units B. 120 units C. 100 units D. 90 or 120 units
Solve.The approach ramp used by a daredevil motorcyclist for flying over a collection of flaming telephone booths has a rise of 45 feet for every 90 feet in horizontal distance. Find the grade of the ramp. Round to the nearest whole percent.
A. 0.5% B. 20% C. 50% D. 55%
Find the slope-intercept form of the equation of the line with the given properties.Horizontal; containing the point 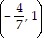
A. y = 1
B. y = - 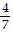
C. y = -1
D. y = 0