Atmospheric air at a velocity of 61 m/s and a temperature of 16°C enters a 0.61-m-long square metal duct of 20 × 20 cm cross section. If the duct wall is at 149°C, determine the average heat transfer coefficient. Comment briefly on the L/Dh effect.
GIVEN
Atmospheric air flow through a square metal duct
Air velocity (V) = 61 m/s
Inlet air temperature (Tb,in) = 16°C
Duct dimensions: 20 cm × 10 cm × 0.61 m = 0.2 m × 0.2 m × 0.61 m
Duct wall surface temperature (Ts) = 149°C
FIND
The average heat transfer coefficient (c h)
ASSUMPTIONS
Steady state
Constant and uniform wall surface temperature
SKETCH
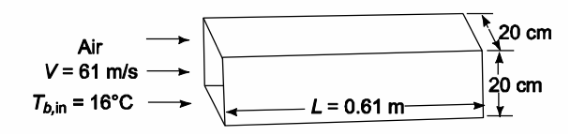
The hydraulic diameter of the duct is given
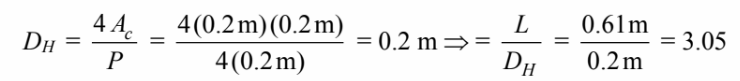
The Reynolds number based on the hydraulic diameter is
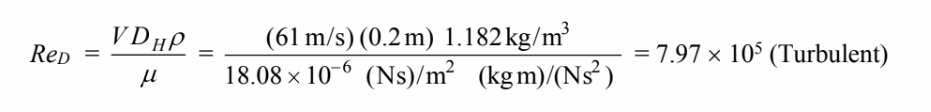
Using the Sieder-Tate correlation with the hydraulic diameter
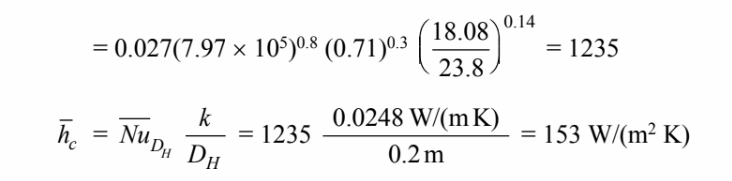
Note that since 2 < L/DH < 20, the heat transfer coefficient will be
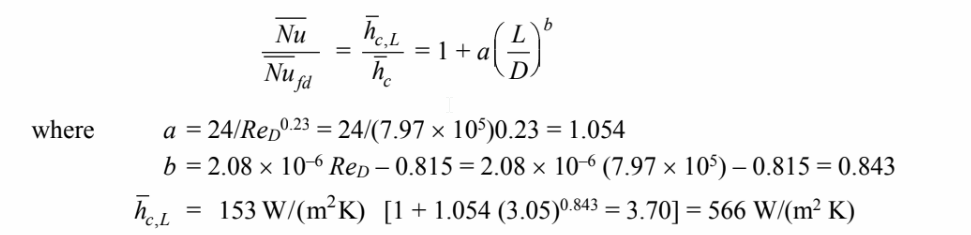
The air properties at the inlet temperature were used in the calculation. This may lead to significant
errors if the air temperature rises appreciably within the duct, therefore, the outlet air temperature will
be calculated. The outlet temperature can be calculated using
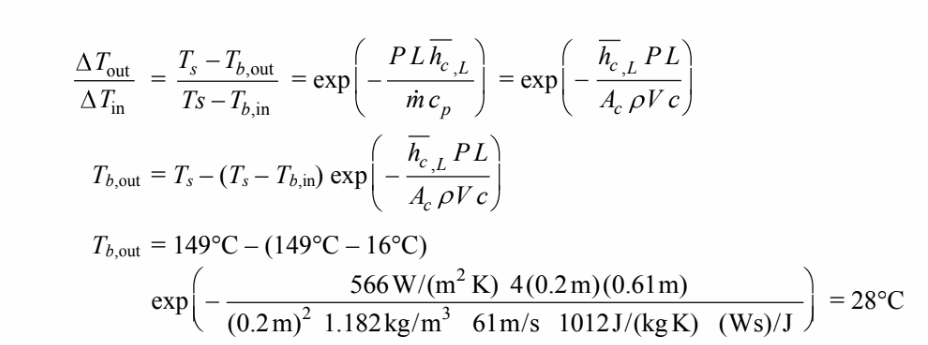
Therefore, the average air temperature is about 22°C. The difference in air properties at 22°C and
16°C is not great enough to justify another iteration.
You might also like to view...
An airplane flies in a semi-circular arc in order to simulate “weightlessness” for its occupants. If the radius of the semicircular path it flies is 3500 m, what is the speed at which the plane flies?
A. 357 m/s B. 580 m/s C. 185 m/s D. 1180 m/s
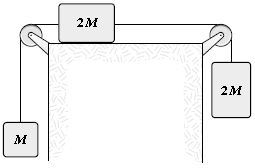
The three blocks shown are released from rest and are observed to move with accelerations that have a magnitude of 1.5 m/s2. What is the magnitude of the friction force on the block that slides horizontally? Disregard any pulley mass or friction in the pulley and let M = 2.0 kg
a.
6.0 N
b.
5.1 N
c.
5.5 N
d.
4.6 N
e.
3.7 N
A mass attached to the end of a spring is pulled out and released on a surface with friction. The work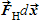
A. ?has the same sign as the change in energy owing to friction during one half of each cycle. B. ?never has the same sign as the change in energy owing to friction. C. ?always has the same sign as the change in energy owing to friction. D. ?never has the same sign as the change in energy owing to friction if the force of friction is greater than the spring force. E. ?always has the same sign as the change in energy owing to friction if the force of friction is greater than the spring force.
Imagine that you could magically move the moon closer to Earth, so that the distance from Earth to moon is cut in half. This would cause the force that Earth exerts on the moon to be
A) reduced to 1/4 of its original value. B) doubled. C) increased to four times its original value. D) halved. E) Nonsense--Earth exerts no force on the moon.