Provide an appropriate response.On a multiple choice test, each question has 6 possible answers. Prove by induction that the number of different ways of completing a test with n questions is 6n.
What will be an ideal response?
Answers may vary. Possible answer:
First, we show the statement is true when n = 1.
When n = 1, 6n = 61 = 6
When n = 1, there is only one question with 6 possible answer . So the number of different ways of completing the test is 6.
So P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is, we assume that Pk is true:
Pk: the number of ways of completing a test with k questions is 6k.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: the number of ways of completing a test with k + 1 questions is 6k+1.
The number of possible answers to the (k + 1)st question is 6. So for any given way of completing the first k questions, there are 6 ways of completing the (k + 1)st question.
The number of ways of completing all k + 1 questions
= 6 ? the number of ways of completing the first k questions = 6 ? 6k = 6k+1
So Pk+1 is true if Pk is assumed true. Therefore, by the principle of mathematical induction, the number of different ways of completing a test with n questions is 6n.
You might also like to view...
Solve the problem.Find the equation for the tangent plane to the surface  at the point
at the point 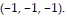
A. -10x - 10y + 12z = 8 B. x + y + z = 8 C. x + y + z = 1 D. -10x - 10y + 12z = 1
Integrate the function.
A. 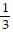
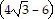
B. 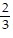
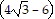
C. 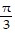
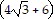
D. 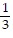
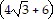
Solve the problem.A section of roller coaster track has the dimensions shown in the diagram. Find the grade of the track, written as a percent. 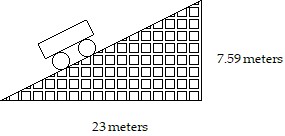
A. 7.59% B. 33% C. 3% D. 38%
Solve the problem using Bayes' Theorem. Round the answer to the nearest hundredth, if necessary.For two events M and N, P(M) = .3, P(N|M) = .4, and P(N|M') = .4. Find P(M'|N).
A. 1.0 B. .30 C. 0 D. .70