Use mathematical induction to prove the statement is true for all positive integers n.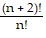
= (n + 2)(n + 1)
What will be an ideal response?
Answers may vary. Possible answer:
First we show that the statement is true when n = 1.
For n = 1, we get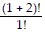 
= (1 + 2)(1 + 1)
Since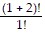 
= 
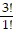= 6 = 3 ? 2 = (1 + 2)(1 + 1), P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
Pk: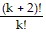 
= (k + 2)(k + 1) is assumed true.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: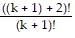 
= ((k + 1) + 2)((k + 1) + 1)
So we assume that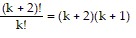 
is true and multiply both sides of the equation by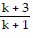 
? 
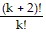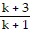= (k + 2)(k + 1) ?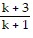 
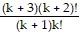= (k + 2)(k + 3) 
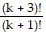= (k + 2)(k + 3)
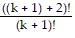= ((k + 1) + 2)((k + 1) + 1)
The last equation says that Pk+1 is true if Pk is assumed to be true. Therefore, by the principle of mathematical induction, the statement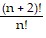 
= (n + 2)(n + 1) is true for all natural numbers n.
You might also like to view...
Provide an appropriate response.Performing systematic operations so that the variable is alone on one side of an equation is known as:
A. an offset with new variables B. offsetting the variable C. a change to new variables D. isolating the variable
Solve. If necessary, round percents to the nearest tenth, dollar amounts to the nearest cent, and all other numbers to the nearest whole.Last year, Lily bought a share of stock for $8.24. She was paid a dividend of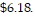 
Determine what percent of the stock price is the dividend.
A. 7.5% B. 1.3% C. 75% D. 25%
Solve the problem.A farmer has 400 yards of fencing to enclose a rectangular garden. Express the area A of the rectangle as a function of the width x of the rectangle. What is the domain of A?
A. A(x) = -x2 + 200x; {x|0 < x < 400} B. A(x) = -x2 + 200x; {x|0 < x < 200} C. A(x) = x2 + 200x; {x|0 < x < 200} D. A(x) = -x2 + 400x; {x|0 < x < 400}
y?? +16y = 8x ? 32, y (0) = 4, y?(0) = 3 8
Solve the initial-value problem.