Provide an appropriate response.The Cobb-Douglas production function for a company is given by 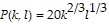 where P is the monthly production value when k is the number of units of capital and l is the number of units of labor. Suppose that capital costs $150 per unit, labor costs $225 per unit, and the total cost of capital and labor is limited to $270,000. Use Lagrange multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
where P is the monthly production value when k is the number of units of capital and l is the number of units of labor. Suppose that capital costs $150 per unit, labor costs $225 per unit, and the total cost of capital and labor is limited to $270,000. Use Lagrange multipliers to write the system of equations you would use to find the number of units of capital and labor that maximize production.
What will be an ideal response?
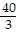 k-1/3l1/3 - 150? = 0 k-1/3l1/3 - 150? = 0 |
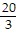 k2/3l-2/3 - 225? = 0 k2/3l-2/3 - 225? = 0 |
| 150k + 225l - 270,000 = 0 |
Mathematics
You might also like to view...
This double-bar graph shows the number of male (M) and female (F) athletes at a university over a four-year period. Answer the question. How many students were involved in athletics in Year 4?
How many students were involved in athletics in Year 4?
A. 750 B. 825 C. 775 D. 800
Mathematics
Solve the system by graphing. 3x + y = -9 5x + 3y = -11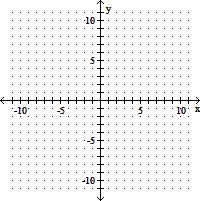
A. (-2, -3) B. (-4, 3) C. (-4, -5) D. (4, 3)
Mathematics
For the given pair of points, find the equation of the line 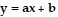 that goes through the points by solving a system of equations.(-9, -7) and (-7, -3)
that goes through the points by solving a system of equations.(-9, -7) and (-7, -3)
A. y = 4x + 11 B. y = 2x + 11 C. y = 2x - 25 D. y = 2x - 7
Mathematics
Solve the equation.e2x = 7
A. {2 ln 7}
B. 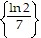
C. 
D. 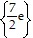
Mathematics