Graph the function. Identify the vertex, x-intercepts, and the equation for the axis of symmetry.f(x) = (x - 1)2 - 9
A. 
vertex: (- 1, - 9)
x-intercepts: (-2, 0) and (4, 0)
axis of symmetry: x = - 1
B. 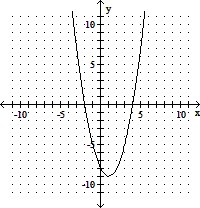
vertex: (1, - 9)
x-intercepts: (-2, 0) and (4, 0)
axis of symmetry: x = 1
C. 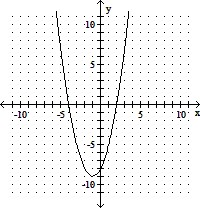
vertex: (- 1, - 9)
x-intercepts: (-4, 0) and (2, 0)
axis of symmetry: x = - 1
D. 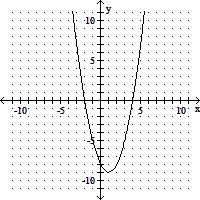
vertex: (1, - 9)
x-intercepts: (2, 0) and (4, 0)
axis of symmetry: x = 1
Answer: B
You might also like to view...
Identify the rules of algebra illustrated from left to right by the following statement. (z? - 7) + 7 = z + (-7 + 7) = z + 0 = z
A. commutative property of addition; additive inverse property; additive identity property B. associative property of addition; additive inverse property; additive identity property C. commutative property of addition; additive identity property; additive inverse property D. associative property of addition; additive identity property; additive inverse property E. distributive property; additive identity property; additive inverse property
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.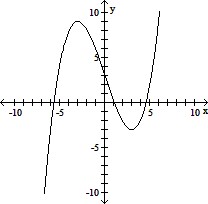
A. Local minimum at x = 3 ; local maximum at x = -3 ; concave up on (-?, -3) and (3, ?); concave down on (-3, 3) B. Local minimum at x = 3 ; local maximum at x = -3 ; concave up on (0, ?); concave down on (-?, 0) C. Local minimum at x = 3 ; local maximum at x = -3 ; concave down on (0, ?); concave up on (-?, 0) D. Local minimum at x = 3 ; local maximum at x = -3 ; concave down on (-?, -3) and (3, ?); concave up on (-3, 3)
Solve.A Ferris wheel has a radius r of 25.7 feet. The height of the tower t is 36.6 feet. The distance d from the origin to the base is 25.9 feet. Find the standard form equation of the circle represented by the Ferris wheel. 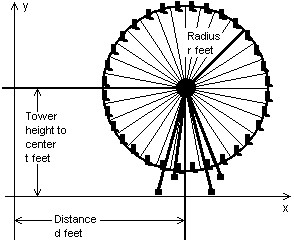
A. (x - 25.9)2 + (y - 36.6)2 = 25.7 B. (x + 25.9)2 + (y + 36.6)2 = 660.49 C. (x - 25.9)2 + (y - 36.6)2 = 660.49 D. (x + 25.9)2 + (y + 36.6)2 = 25.7
Find all cube roots of the complex number. Leave answers in trigonometric form.2 + 2i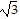
A.  cis 20°,
cis 20°,  cis 140°,
cis 140°, 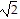 cis 260°
cis 260°
B.  cis 20°,
cis 20°, 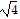 cis 140°,
cis 140°,  cis 260°
cis 260°
C.  cis 30°,
cis 30°,  cis 150°,
cis 150°,  cis 270°
cis 270°
D.  cis 20°,
cis 20°,  cis 140°,
cis 140°, 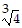 cis 260°
cis 260°