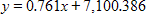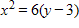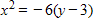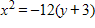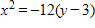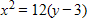For the following numbers, (i) use a calculator to add; and (ii) estimate the sum by rounding the numbers to the nearest ten-thousand and adding.
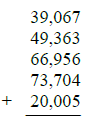
A) (i) 259,195 ; (ii) 240,000
B) (i) 239,085 ; (ii) 270,000
C) (i) 259,195 ; (ii) 250,000
D) (i) 249,095 ; (ii) 240,000
E) (i) 249,095 ; (ii) 250,000
E) (i) 249,095 ; (ii) 250,000
You might also like to view...
Write the expression in lowest terms.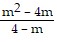
A. -m B. m + 2 C. m D. -(m + 2)
Complete the ordered pairs. Then graph the equation by plotting the points and drawing a line through them.2x - y = -4(0, ), ( , 0), (4, )
A. (0, 4), (8, 0), (4, 6)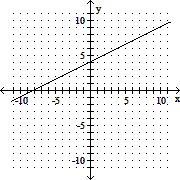
B. (0, 4), (2, 0), (4, -4)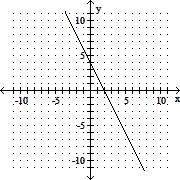
C. (0, 4), (-2, 0), (4, 12)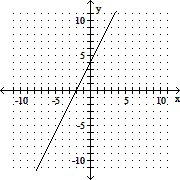
D. (0, -4), (2, 0), (4, 4)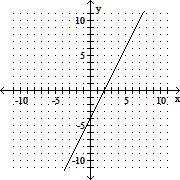
The table gives the median household income (in 2005 year) for two cities in various years. Let x represent the median household income for citizens of city A and y represent the corresponding median household income for citizens of city B. Find a linear model that expresses the median household income for citizens in city B as a function of the median household income for citizens of city B. Interpret the slope of the linear model. Round numerical values in your answer to three decimal places. Median Household Income(2005 year)Year City A City B 1985 $21,900 $19,600 1990 $23,800 $21,500 1995 $25,700 $24,500 2000 $27,400 $27,200 2005 $31,000 $31,100
A.
slope: median household income is growing at the same rate for city A as it is for city B.
B.
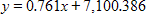
slope: median household income is growing at the same rate for city A as it is for city B.
C.
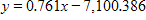
slope: median household income is growing at the same rate for city A as it is for city B.
D.
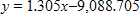
slope: median household income is growing faster for city A than it is for city B.
E.
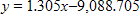
slope: median household income is growing slower for city A than it is for city B.
Find the standard form of the equation of the parabola with the given characteristics.
?
Focus: 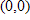
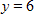
A.
B.
C.
D.
E.