Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.5 + 5 ? 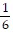 + 5 ?
+ 5 ? 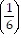 2 + ... + 5 ?
2 + ... + 5 ? 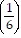 n - 1 =
n - 1 = 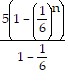
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 3 = 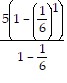 = 3.
= 3.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
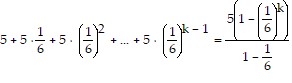 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
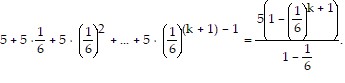
So we assume that 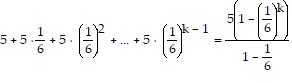 is true and add the next term,
is true and add the next term, 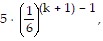 to both sides of the equation.
to both sides of the equation.
5 + 5 ? 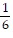 + 5 ?
+ 5 ? 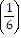 2 + ... + 5 ?
2 + ... + 5 ? 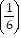 k - 1 + 5 ?
k - 1 + 5 ? 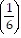 (k + 1) - 1=
(k + 1) - 1= 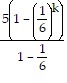 + 5 ?
+ 5 ? 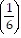 (k + 1) - 1
(k + 1) - 1
= 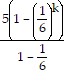 + 5
+ 5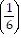 k
k
= 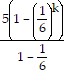 +
+ 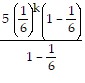
= 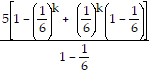
= 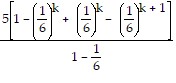
= 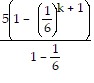
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem.The position of an object moving in a straight line is given by 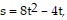 where s is in meters and t is the time in seconds the object has been in motion. How far will an object move in 8 seconds?
where s is in meters and t is the time in seconds the object has been in motion. How far will an object move in 8 seconds?
A. 32 m B. 256 m C. 480 m D. 192 m
Match the given equation with one of the graphs.(x + 2)2 = 4(y + 2)
A. 
B. 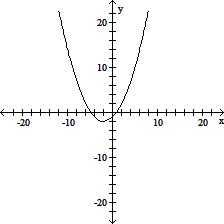
C. 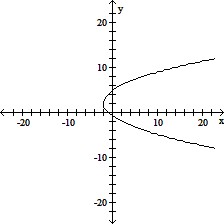
D. 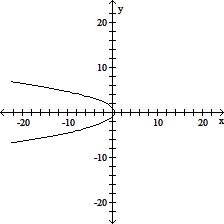
Establish the identity.cot 2 x + csc 2 x = 2 csc 2 x - 1
What will be an ideal response?
Divide.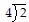
A. 1.5 B. 15 C. 5 D. 0.5