Solve the given differential equation.D4y + 18 D2y + 81y = 0
A. y = c1 sin 3x + c2 cos 3x
B. y = (c1 + c2x)sin 3x + (c3 + c4x)cos 3x
C. y = (c1 + c2x)sin x + (c3 + c4x)cos x
D. y = (c1 + c2x)sin 3x + (c3 + c4x)ex
Answer: B
You might also like to view...
Find the unit tangent vector of the given curve.r(t) = (10 - 2t)i + (2t - 8)j + (7 + t)k
A. T = 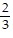 i -
i - 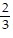 j -
j - 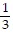 k
k
B. T = - 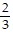 i +
i + 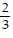 j +
j + 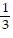 k
k
C. T = 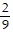 i -
i - 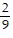 j -
j - 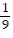 k
k
D. T = - 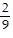 i +
i + 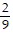 j +
j + 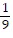 k
k
Find the slope of the line (if it exists) and the y-intercept (if it exists).3x - 9y = -18
A. Slope -3, y-intercept (0, 2)
B. Slope  , y-intercept (0, 2)
, y-intercept (0, 2)
C. Slope 3, y-intercept (0, -2)
D. Slope - 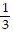 , y-intercept (0, -2)
, y-intercept (0, -2)
Solve the problem.The arch beneath a bridge is semi-elliptical, a one-way roadway passes under the arch. The width of the roadway is 38 feet and the height of the arch over the center of the roadway is 11 feet. Two trucks plan to use this road. They are both 8 feet wide. Truck 1 has an overall height of  and Truck 2 has an overall height of
and Truck 2 has an overall height of 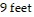 . Draw a rough sketch of the situation and determine which of the trucks can pass under the bridge.
. Draw a rough sketch of the situation and determine which of the trucks can pass under the bridge.
A. Truck 2 can pass under the bridge, but Truck 1 cannot. B. Truck 1 can pass under the bridge, but Truck 2 cannot. C. Both Truck 1 and Truck 2 can pass under the bridge. D. Neither Truck 1 nor Truck 2 can pass under the bridge.
Construct a frequency table for the given data.The following is the number of bonus points that 24 students have gotten for extra work. Use six intervals, starting with 0 - 49.48 74 127 185 223 206 163 102 75 33 83 25392 104 191 227 199 114 50 100 150 199 160 283
A. 
B. 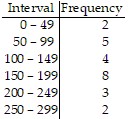
C. 
D. 