Solve the problem.Under what circumstances is the Average Daily Balance method a more favorable method to the borrower than the Unpaid Balance method? Explain.
What will be an ideal response?
The average daily balance method is more favorable to the borrower than the Unpaid Balance method when the borrower's partial payments exceed the new charges during the current billing cycle. This negative balance will serve to reduce the finance charges in the average daily balance method but will not change the finance charges at all in the unpaid balance method.
You might also like to view...
Solve the problem.Find the tangent line(s) at the pole for the curve 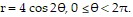
A. ? = 0 (y = 0), ? = 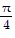 (y = x), ? =
(y = x), ? =  (x = 0), ? =
(x = 0), ? = 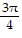 (y = -x)
(y = -x)
B. ? = 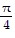 [y =
[y =  x], ? =
x], ? = 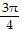 [y = -
[y = -  x]
x]
C. ? = 0 (y = 0), ? = 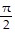 (x = 0)
(x = 0)
D. ? =  (y = x), ? =
(y = x), ? =  (y = -x)
(y = -x)
Answer the question.Your true height is 70.4 inches. A tape measure that can be read to the nearest tenth of an inch gives your height as 70.5 inches. A second tape measure which can be read to the nearest eighth of an inch gives your height as 70 inches. Which of these two measurement is more precise? Which is more accurate?
inches. Which of these two measurement is more precise? Which is more accurate?
A. The first tape measure gives a more precise reading but the second tape measure gives a more accurate reading. B. The second tape measure gives a more precise reading and also a more accurate reading. C. The second tape measure gives a more precise reading but the first tape measure gives a more accurate reading. D. The first tape measure gives a more precise reading and also a more accurate reading.
List the terms of the expression. Then identify the coefficient of each term.3c2 - 7c - nt
A. 3c2, -7c, -nt; 3, -7, -1 B. 3c2, 7c, nt; 3, 7, 1 C. -3c2, -7c, -n, t; 3, -7, -1, 1 D. -3c2, -7c, -nt; 3, 7, 1
Find all the complex roots. Write the answer in the indicated form.The complex cube roots of 125(cos 273° + i sin 273°) (polar form)
A. -5(cos 91° + i sin 91°), 5(cos 211° + i sin 211°), -5(cos 331° + i sin 331°) B. 5(cos 91° + i sin 91°), 5(cos 131° + i sin 131°), 5(cos 171° + i sin 171°) C. -5(cos 91° + i sin 91°), 5(cos 131° + i sin 131°), -5(cos 171° + i sin 171°) D. 5(cos 91° + i sin 91°), 5(cos211° + i sin 211°), 5(cos 331° + i sin 331°)