Solve the problem.The annual population density of a species of insect after n years is modeled by a sequence. Suppose that the initial density of insects is 624 with r = 0.6. Write a recursive sequence that describes this data, where an denotes the insect density during year n.Find the terms a1 , a2 , a3 , ...... until you are able to interpret the results.
A. The population density increases by 60% each year.
B. The population density decreases by 40% each year.
C. The population density increases by 40% each year.
D. The population density decreases by 60% each year.
Answer: B
You might also like to view...
Answer the question.Which of the following is not a condition for applying the integral test to the sequence {an}, where an = f(n)?
A. f(x) is continuous for x ? N B. f(x) is decreasing for x ? N C. f(x) is everywhere positive D. All of these are conditions for applying the integral test.
Use integration by parts to establish a reduction formula for the integral.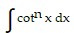 , n ? 1
, n ? 1
A.  =
=  cotn-1 x -
cotn-1 x - 
B. 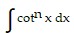 =
= 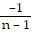 cotn-2 x -
cotn-2 x - 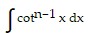
C.  = - cotn-1 x +
= - cotn-1 x + 
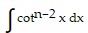
D.  =
=  cotn-1 x +
cotn-1 x + 
Solve.A large crater on the moon is approximately circular. The depth (in feet) of the crater below any point on a diameter can be modeled by the expression 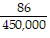 (x2 - 300x - 100,000), where x is the distance to the point on the diameter 1000 feet in from the edge. Write this expression in factored form.
(x2 - 300x - 100,000), where x is the distance to the point on the diameter 1000 feet in from the edge. Write this expression in factored form.
A. 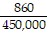 (x - 20)(x + 100)
(x - 20)(x + 100)
B. 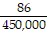 (x + 200)(x - 500)
(x + 200)(x - 500)
C. 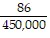 (x - 200)(x + 500)
(x - 200)(x + 500)
D. 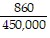 (x + 20)(x - 50)
(x + 20)(x - 50)
Solve the equation.|x| = -5
A. {-5} B. {5} C. no solution D. {5, -5}