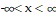The number of bacteria in a culture is increasing according to the law of exponential growth. After 1 hour0 there are 135 bacteria in the culture and after 2 hours there are 395 bacteria in the culture. Answer the following questions, rounding numerical answers to four decimal places.
?
(I) Find the initial population.
?
(II) Write an exponential growth model for the bacteria population. Let t represent time in hours.
?
(III) Use the model to determine the number of bacteria after 4 hours.
?
(IV) After how many hours will the bacteria count be 10,000?
?
A. (I) 46.1397; (II)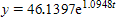 
; (III) 4,694.2310; (IV) 7.3444 hr
B. (I) 48.2897; (II)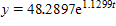 
; (III) 6,068.9482; (IV) 9.5724 hr
C. (I) 46.1397; (II)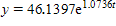 
; (III) 3,381.4969; (IV) 5.0099 hr
D. (I) 51.9197; (II)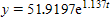 
; (III) 8,820.4016; (IV) 11.6836 hr
E. (I) 53.4797; (II)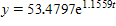 
; (III) 11,472.8651; (IV) 13.463 hr
Answer: C
You might also like to view...
Solve for the variable.11 + x = -14
A. -3 B. -25 C. 25 D. 3
Find the x-intercepts.y = 4x2 - 7x
A. (0, 0) and (0, 1.75) B. (1.75, 0) C. (0, 0) and (1.75, 0) D. (0, 0) and (-1.75, 0)
Factor the trinomial completely.u2 - 3uv - 54v2
A. (u + 6v)(u - 9v) B. (u - v)(u + 9v) C. (u - 6v)(u + v) D. (u - 6v)(u + 9v)
Find the nth-degree Taylor polynomial at 0 for f, find the Taylor series at 0 for f, and determine the values of x for which 
.f(x) = e-3x
A.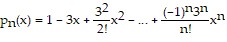 
; 
; 
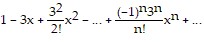B.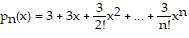 
; 
; 
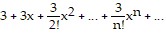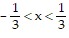
C.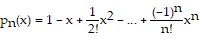 
; 
; 
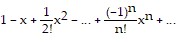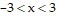
D.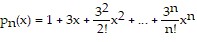 
; 
; 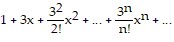