Solve the problem.The logistic growth model 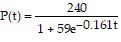 represents the population of a species introduced into a new territory after t years. When will the population be 80?
represents the population of a species introduced into a new territory after t years. When will the population be 80?
A. 18.5 years
B. 6.08 years
C. 21.02 years
D. 8.6 years
Answer: C
You might also like to view...
One of sin x, cos x, and tan x is given. Find the other two if x lies in the specified interval.tan x =  ,
, x in
x in 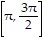
A. sin x =  , cos x =
, cos x = 
B. sin x = - 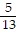 , cos x = -
, cos x = - 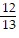
C. sin x = 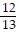 , cos x =
, cos x = 
D. sin x = -  , cos x = -
, cos x = - 
Solve the system of equations by elimination.6x + 36y = 367x - 4y = -4
A. (0, 1) B. (0, 0) C. (1, 0) D. (1, 1)
Discuss the equation and graph it.r = 
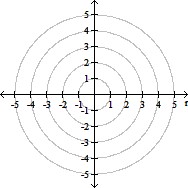
A. directrix parallel to polar
axis 2 below pole
focus (0, 0), vertex 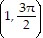

B. directrix perpendicular to polar
axis 2 left of pole
focus (0, 0), vertex 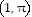

C. directrix perpendicular to polar
axis 2 right of pole
focus (0, 0), vertex 

D. directrix parallel to polar
axis 2 above pole
focus (0, 0), vertex 
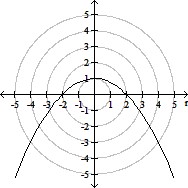
Solve the system of equations using matrices. Use Gaussian elimination with back-substitution.3x + 5y - 2w=-132x + 7z - w=-14y + 3z + 3w=1-x + 2y + 4z=-5
A. {(-1, - 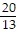 , 0,
, 0, 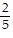 )}
)}
B. {(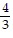 , -
, - 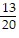 , 0,
, 0, 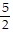 )}
)}
C. {(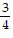 , -2, 0,
, -2, 0, 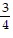 )}
)}
D. {(1, -2, 0, 3)}