Solve the problem.A particle moves along an ellipse in the xy-plane in such a way that its position at time t is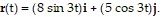 
Find the maximum and minimum values of 
and 
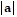. (Hint: Find the extreme values of 
2 and 
2 first and take
square roots later).
A.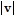 
min = 5; 
max = 8;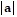 
min = 45; 
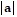max = 72
B.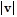 
min = 15; 
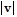max = 24; 
min = 15; 
max = 24
C.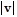 
min = 15; 
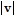max = 24; 
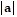min = 45; 
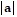max = 72
D.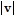 
min = 
max = 24;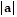 
min = 
max = 72
Answer: C
You might also like to view...
Provide an appropriate response.How are the graphs of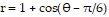 
and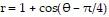 
related to the graph of 
In general, how is the graph of r = f(? - ?) related to the graph of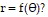 
What will be an ideal response?
Find all the second partial derivatives.f(x, y) = cos xy2
A.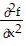 
= -y4 cos xy2; 
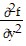= -2x[2xy2 cos(xy2) + sin(xy2)]; 
= 
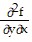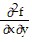= -2y[xy2 cos(xy2) + sin(xy2)]
B.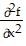 
= - y2 sin xy2; 
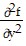= 2y
; 
= 
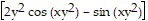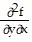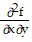= 2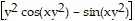
C.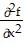 
= - y2 sin xy2; 
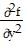= 2[ sin (xy2) - 2y2 cos (xy2)]; 
= 
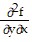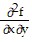= 2y [sin (xy2) - y2 cos (xy2)]
D.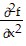 
= y2 sin xy2; 
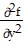= 2[2y2 cos (xy2) - sin (xy2)]; 
= 
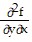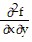= 2y[y2 cos (xy2) - sin (xy2)]
Provide an appropriate response.Perform the indicated operation, leaving the answer in lowest terms: 7 ×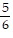 
=
A.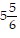 
B.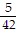 
C. 2
D.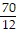 
List the intercepts for the graph of the equation.y = x3 - 64
A. (0, -4), (0, 4) B. (0, -4), (-4, 0) C. (-64, 0), (0, 4) D. (0, -64), (4, 0)