For the graph below, use the nearest neighbor algorithm to find an approximate minimum Hamilton circuit and its weight, starting at the indicated vertex.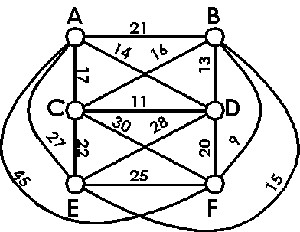
Starting at D
A. D ? C ? B ? F ? E ? A ? D; weight = 102
B. D ? C ? B ? F ? A ? E ? D; weight = 99
C. D ? C ? B ? F ? E ? A ? D; weight = 99
D. D ? C ? A ? F ? E ? B ? D; weight = 102
Answer: A
You might also like to view...
The graph of the given function is drawn with a solid line. The graph of a function, g(x), transformed from this one is drawn with a dashed line. Find a formula for g(x).f(x) =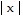 
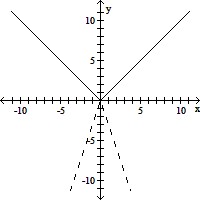
A. g(x) =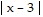 
B. g(x) = -3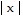
C. g(x) =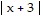 
D. g(x) =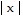 
- 3
List the factors of the number.28
A. 1, 2, 4, 7, 14, 28 B. 1, 2, 7, 14, 28 C. 1, 2, 4, 7, 8, 14, 28 D. 2, 7, 14, 28
Use Pascal's triangle to expand the binomial.(x - 5y)5
A. x5 - 25x4y + 500x3y2 - 2500x2y3 + 3125xy4 - 5y5 B. x5 - 25x4y + 250x3y2 - 1250x2y3 + 3125xy4 - 3125 C. x5 - 25x4y + 500x3y2 - 2500x2y3 + 3125xy4 - 3125y5 D. x5 - 25x4y + 250x3y2 - 1250x2y3 + 3125xy4 - 3125y5
Solve the problem.The amount of a certain drug in the bloodstream is modeled by the function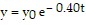 
, where y0 is the amount of the drug injected (in milligrams) and t is the elapsed time (in hours). Suppose that 10 milligrams are injected at 10:00 A.M. If a second injection is to be administered when there is 1 milligram of the drug present in the bloodstream, approximately when should the next dose be given? Express your answer to the nearest quarter hour.
A. 5: 30 P.M B. 3:45 P.M C. 12:30 P.M D. 5:45 P.M