A circumferential fin with a rectangular cross section is made of mild steel has an outer diameter of 3.7 cm OD, and a thickness of 0.3 cm. An array of these circular fins 5 are attached to a circular tube with an outer diameter of 2.5 cm as shown. Cooling air blowing over the fin produces a heat transfer coefficient of 28.4 W/(m2 K). If the temperatures of the base of the fin and of the flowing air are 260°C and 38°C, respectively, numerically determine the temperature distribution in the fin and the heat transfer rate from the fin. Compare your results with those obtained by fin analysis of Chapter 2. Also, how different is the performance if the fins are made of aluminum instead?
GIVEN
- Circumferential fin of mild steel with rectangular cross section.
- Fin outer diameter (do)= 3.7 cm=0.037 m
- Fin thickness(t)= 0.3 cm =0.003 m
- Tube outer diameter (di)=2.5 cm=0.025 m
- Convection heat transfer coefficient(h c)= 28.4 W/(m2 K)
- Temperature of fin base (Tb)= 2600C
- Ambient temperature (T?)= 380C
FIND
(a) Temperature distribution in fin
(b) Rate of heat transfer in fin
(c) Difference in performance when fins are made of aluminum instead.
PROPERTIES
From Appendix 2 Table
- Thermal conductivity of mild steel(k)= 43 W/(m K)
- Thermal conductivity of Aluminum (k)=238 W/(m K)
SKETCH
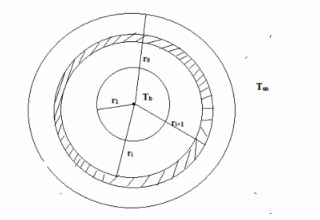
For the node and control volume arrangement shown in the sketch, we have
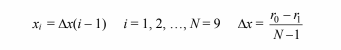
For the control volume at i = 1, we have a specified temperature, therefore
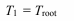
For the interior control volumes, i = 2, 3, 4, 5,... , 8 an energy balance gives
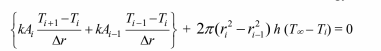
Where Ai=2?rit
Writing this in the tridiagonal form
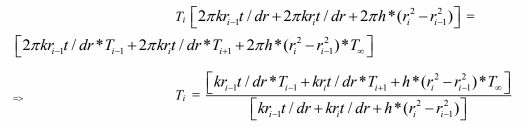
Neglecting heat loss from tip of the fin as fin thickness is very small we have
TN=TN-1
and T1=Tb as boundary conditions
The above problem is solved by discretization method using matlab. The matlab code is given below.
% Matlab code for problem_4_54
L=6*10^-3; % in m
N=11;
delr=L/(N-1); % in m
t=0.003; % in m
h=28.4; % W/(m^2 K)
k=43; % W/(m K)
T(1)=260; % Celsius
T(2:N)=0; % Celsius
Tinf=38; % Celsius
for i=1:N
r(i)=(0.0125+(i-1)*delr);
end
for j=1:1:300
for i=N-1:-1:2
Tf=T;
T(i)=(k*r(i-1)*t/delr*T(i-1)+k*r(i)*t/delr*T(i+1)+h*(r(i)^2-r(i-
1)^2)*Tinf)/(k*r(i-1)/delr*t+k*r(i)/delr*t+h*(r(i)^2-r(i-1)^2));
T(N)=T(N-1);
end;
count=0;
for i=1:N
if abs(Tf(i)-T(i))<10^-5
count=count+1;
end
end
if count==N
break
end
end
for i=1:1:N
x(i)=(i-1)*delr;
end
plot(x,T)
q=k*2*pi*r(1)*t*(T(1)-T(2))/delr
The temperature distribution found through above discretization in matlab is given below
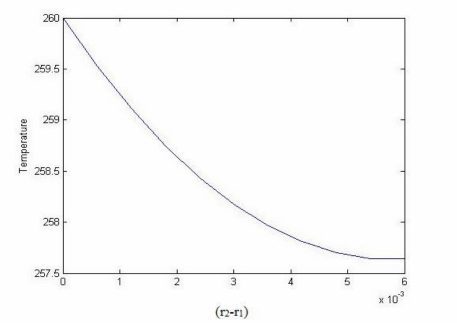
The heat flow through the fin is given by conduction through first control volume which is calculated
as
Q= k*2?*r1*t*(T(1)-T(2))/?r
which is obtained as Q= 8.104 Watt
Now, from chapter 2.
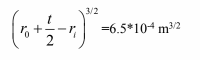
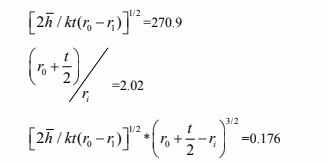
From figure 2.22 for efficiency of circumferential fins
From figure 2.22 for efficiency of circumferential fins
?f=98%
Thus the heat transfer through the fin is given by
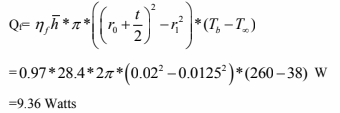
which is near to the discretization solution we obtained through matlab. If Aluminum is used instead
of mild steel. Substituting the value of thermal conductivity in above matlab code we get
You might also like to view...
Waves on a String: A crane lifts a 2500-kg beam using a steel cable whose mass per unit length is 0.650 kg/m. What is the speed of transverse waves on this cable if the upward acceleration of the beam is a steady 3.00 m/s2?
A. 194 m/s B. 578 m/s C. 1220 m/s D. 1880 m/s E. 222 m/s
Two balls of different material, but the same radius, ball A and ball B, float on the surface of a pool filled with fresh water of 1000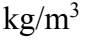
density. If ball A has 45% of its volume above the water, and ball B has 55% of its volume above the water, what is the ratio of the mass of ball A to that of B?
A. 0.905 B. 1.07 C. None of these D. 1.22 E. 0.82 F. 0.935
The Lewis symbol X• would be characteristic of which group?
a. 2A b. 4A c. 6A d. 1A
A star with a parallax angle of 1/20 arcsecond is ________
A) 20 parsecs away B) 20 light-years away C) 10 parsecs away D) 1/20 parsec away