A tennis racket manufacturer produces two types of rackets, standard and competition. The weekly revenue function, in dollars, for x standard rackets and y competition rackets is given by R(x, y) = 54x + 2xy + 398y - 2x2 - 9y2i) How many of each type of racket must be produced each week to maximize revenue?ii) What is the maximum weekly revenue?
A. i) 25 standard rackets and 26 competition rackets;
ii) $5664
B. i) 26 standard rackets and 25 competition rackets;
ii) $5677
C. i) 25 standard rackets and 25 competition rackets;
ii) $5675
D. i) 26 standard rackets and 26 competition rackets;
ii) $5668
Answer: B
You might also like to view...
Set up the general equation from the given statement.D varies directly as r and is inversely proportional to 
.
A. D = kr +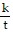 
B. D = 
C. D = krt
D. D = k(r + t)
Choose the graph that satisfies the given conditions.Quartic polynomial with one x-intercept and a positive leading coefficient
A.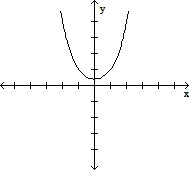 
B.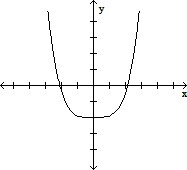 
C.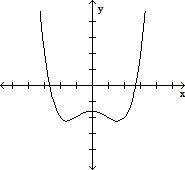 
D.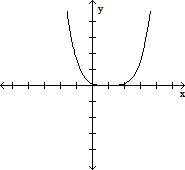 
Answer the question.For f(x) = 8x + 7 and g(x) = 2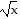
, what is the domain of g?f?
A.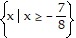 
B.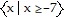 
C. All real numbers
D.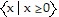 
Solve the problem.A rectangular garden has dimensions of 23 feet by 13 feet. A gravel path of equal width is to be built around the garden. How wide can the path be if there is enough gravel for 576 square feet?
A. 8.5 ft B. 6 ft C. 8 ft D. 7 ft