Identify the initial amount "a" and the rate of growth "r" (as a percent) of the exponential function. Evaluate the function when t = 5. Round your answer to the nearest tenth
What will be an ideal response?
Answer:
Initial amount = 1
Rate of growth = 80 %
The value is 18.9 when t = 5
Solution:
The given exponential function is:
p(t) = 1.8^t
The exponential function is given as:
y = a(1+r)^t
Where,
y is the future value
a is the initial value
r is the growth rate
t is the number of years
Compare both the functions,
a = 1
1+r = 1.8
r = 1.8 - 1
r = 0.8
Thus growth rate is:
r = 0.8 = 0.8 \times 100 \% = 80 \%
Evaluate the function when t = 5
Substitute t = 5 in given
p(5) = 1.8^5
p(5) = 18.89568 approx 18.9
Thus the value is 18.9 when t = 5
You might also like to view...
Round the money amount to the specified place.$99.52 to the nearest dollar
A. $100 B. $99 C. $99.52 D. $9
Find the product.-5n7(9n7 - 5n4)
A. -45n14 - 25n11 B. -45n14 + 25n11 C. -45n2 + 25n D. -45n14 - 5n4
Divide using synthetic division, and write a summary statement in fraction form.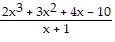
A. 2x2 + x - 3 + 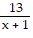
B. 2x2 + 5x + 9 + 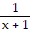
C. 2x2 + x + 3 - 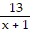
D. 2x2 + 5x + 9 + 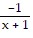
Decide whether the relation is a function.{(-3, 2), (2, -4), (5, -1), (8, 4), (11, -2)}
A. Not a function B. Function