Divide f(x) by g(x) and write in the form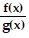 
= quotient + 
.f(x) = x4 + 3x3 + 5x2 + 3x + 4; g(x) = x2 + 1
A. x2 - 3x + 4 +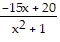 
B. x2 - 3x + 4
C. x2 + 3x + 4
D. x2 + 3x + 4 +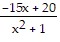 
Answer: C
You might also like to view...
Divide. Express the quotient in lowest terms.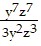
÷ 
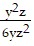
A. 
B. 
C.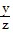 
D. 2y4z5
Refer to the weighted voting system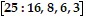 
and the Banzhaf definition of power. (The four players are P1, P2, P3 and P4.)The weight of the coalition {P1, P2, P3, P4} is
A. 33. B. 34. C. 39. D. 17. E. none of these
Solve.Suppose economists use as a model of a country's economy the function N(x) = 0.6898x + 5.9243,where N represents the consumption of products in billions of dollars and x represents disposable income in billions of dollars. a. Identify the dependent and independent variables.b. Evaluate N(8.67)and explain what it represents.
A. a. The dependent variable is the number of billions of dollars, N, and the independent variable is the disposable income in billions of dollars. b. N(8.67) = $3.8 billion; According to the model, the number of billions of dollars for the consumption of products is $3.8 billion. B. a. The dependent variable is the number of billions of dollars, N, and the independent variable is the disposable income in billions of dollars. b. N(8.67) = $11.9 billion; According to the model, the number of billions of dollars for the consumption of products is $11.9 billion. C. a. The dependent variable is the number of billions of dollars, N, and the independent variable is the disposable income in billions of dollars. b. N(8.67) = $4.0 billion; According to the model, the number of billions of dollars for the consumption of products is $4.0 billion. D. a. The dependent variable is the number of billions of dollars, N, and the independent variable is the disposable income in billions of dollars. b. N(8.67) = $5.2 billion; According to the model, the number of billions of dollars for the consumption of products is $5.2 billion.
Solve the application.Annie must send two packages. One of the packages weighs 14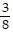
pounds and the other weighs 19
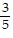pounds. What is the total weight of the two packages?
A. 34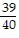
pounds
B. 32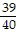
pounds
C. 33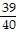
pounds
D. 14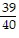
pounds