Calculate the arc length of the indicated portion of the curve r(t).r(t) = (3t sin t + 3 cos t)i + (3 t cos t - 3 sin t)j ; -3 ? t ? 6
A. 67.5
B. 40.5
C. 135
D. 81
Answer: B
You might also like to view...
Evaluate the integral.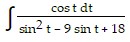
A. 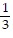 ln
ln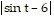 -
- 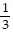 ln
ln 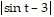 + C
+ C
B. ln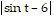 - ln
- ln 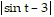 + C
+ C
C. 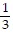 ln
ln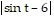 +
+ 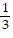 ln
ln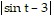 + C
+ C
D. 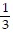 ln
ln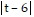 -
- 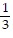 ln
ln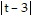 + C
+ C
Solve the problem.A patient takes 100 mg of medication every 24 hours. 80% of the medication in the blood is eliminated every 24 hours.a. Let dn equal the amount of medication (in mg) in the blood stream after n doses, where d1 = 100. Find a recurrence relation for dn.b. Show that 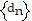 is monotonic and bounded, and therefore converges.c. Find the limit of the sequence. What is the physical meaning of this limit?
is monotonic and bounded, and therefore converges.c. Find the limit of the sequence. What is the physical meaning of this limit?
A. a. dn + 1 = 0.2dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 150 for n ? 1 and its terms are increasing in size. c. 150; in the long run there will be approximately 150 mg of medication in the blood. B. a. dn + 1 = 0.2dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 125 for n ? 1 and its terms are increasing in size. c. 125; in the long run there will be approximately 125 mg of medication in the blood. C. a. dn + 1 = 0.8dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 150 for n ? 1 and its terms are increasing in size. c. 150; in the long run there will be approximately 150 mg of medication in the blood. D. a. dn + 1 = 0.8dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 125 for n ? 1 and its terms are increasing in size. c. 125; in the long run there will be approximately 125 mg of medication in the blood.
Solve the problem.Suppose that the odds of winning the grand prize in a raffle are 1 to 7. What is the probability of winning the grand prize?
A. 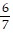
B. 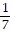
C. 
D. 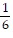
E. none of these
Graph the equations.f(x) = 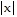 + 1
+ 1
A. 
B. 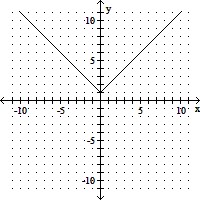
C. 
D. 