Use mathematical induction to prove the statement is true for all positive integers n.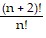 = (n + 2)(n + 1)
= (n + 2)(n + 1)
What will be an ideal response?
Answers may vary. Possible answer:
First we show that the statement is true when n = 1.
For n = 1, we get 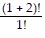 = (1 + 2)(1 + 1)
= (1 + 2)(1 + 1)
Since 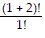 =
=  = 6 = 3 ? 2 = (1 + 2)(1 + 1), P1 is true and the first condition for the principle of induction is satisfied.
= 6 = 3 ? 2 = (1 + 2)(1 + 1), P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
Pk: 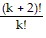 = (k + 2)(k + 1) is assumed true.
= (k + 2)(k + 1) is assumed true.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: 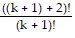 = ((k + 1) + 2)((k + 1) + 1)
= ((k + 1) + 2)((k + 1) + 1)
So we assume that  is true and multiply both sides of the equation by
is true and multiply both sides of the equation by 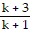
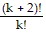 ?
? 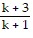 = (k + 2)(k + 1) ?
= (k + 2)(k + 1) ? 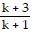
 = (k + 2)(k + 3)
= (k + 2)(k + 3) 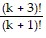 = (k + 2)(k + 3)
= (k + 2)(k + 3)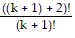 = ((k + 1) + 2)((k + 1) + 1)
= ((k + 1) + 2)((k + 1) + 1)
The last equation says that Pk+1 is true if Pk is assumed to be true. Therefore, by the principle of mathematical induction, the statement 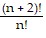 = (n + 2)(n + 1) is true for all natural numbers n.
= (n + 2)(n + 1) is true for all natural numbers n.
You might also like to view...
Solve the problem.Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 4 times as many dimes as nickels, and the value of the dimes is $3.15 more than the value of the nickels. How many nickels and dimes does Jamil have?
A. 36 nickels and 9 dimes B. 8 nickels and 32 dimes C. 10 nickels and 40 dimes D. 9 nickels and 36 dimes
In order to prepare her budget, Sue gathers receipts for all major expenses she has had over the last month. Round the figure to the nearest dollar.Groceries, $438.01
A. $437 B. $438.10 C. $439 D. $438
Evaluate the quotient function at the indicated value.Given g(x) = x3 + 8 and k(x) = x2 - 4, find 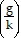 (0).
(0).
A. 4 B. -2 C. 2 D. undefined
Find the LCM.t , t - 1
A. t B. t(t - 1) C. 10 D. t - 1