Solve the problem.A projectile is fired from the top of a building 200 feet high. The graph shows the height of the projectile, in feet, above the ground, in terms of its distance, in feet, from the base of the building. 
Estimate the coordinates of the point A. Interpret the coordinates in terms of the information given.
A. approximately (1350, 200); the projectile is 200 feet above the ground when it is 1350 feet from the base of the building.
B. approximately (1350, 200); the projectile is 1350 feet above the ground 200 seconds after it is fired.
C. approximately (200, 1350); the projectile is 1350 feet from the base of the building 200 seconds after it is fired
D. approximately (1350, 200); the projectile is 1350 feet above the ground when it is 200 feet from the base of the building.
Answer: A
You might also like to view...
Write a recursion formula for the sequence.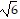
, 6, 36, 1296, . . .
A. an = (an-1)2, a1 =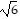 
B. an = 
, a1 =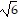 
C. an =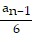 
, a1 =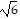 
D. an = 6an-1, a1 =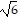 
Add. Write the answer in lowest terms.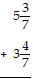
A. 9
B. 9
C. 4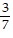
D. 8
Sketch trajectories of solutions of z? = Az given the eigenvalues and associated eigenvectors of A. Classify the origin and assess its stability.
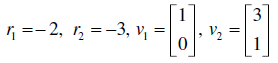
Solve the problem.Two recording devices are set 3400 feet apart, with the device at point A to the west of the device at point B. At a point on a line between the devices, 300 feet from point B, a small amount of explosive is detonated. The recording devices record the time the sound reaches each one. How far directly north of site B should a second explosion be done so that the measured time difference recorded by the devices is the same as that for the first detonation? Round to the nearest hundredth when necessary.
A. 1673.32 ft B. 664.29 ft C. 1517 ft D. 5378.97 ft