Two formulas that approximate the dosage of a drug prescribed for children are: Young's Rule: C =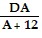 
and Cowling's Rule: C = 
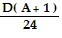.In each formula, A = the child's age in years, D = an adult dosage, and C = the proper child's dosage. The formulas apply for ages 2 through 13. Use these formulas to solve the problem.Use Cowling's Rule to find the difference in a child's dosage for a 9-year-old child and a 6-year old child. Express the answer as a single rational (or fractional) expression in terms of D.
A.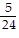 
D
B. 3D
C. 
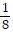D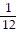
D. 
D
Answer: C
You might also like to view...
Describe the value chain and explain how a company might use value chain analysis to support decisions about outsourcing.
What will be an ideal response?
Use the Intermediate Value Theorem to determine whether the polynomial function has a zero in the given interval.f(x) = 10x3 - 4x2 - 10x - 9; [1, 2]
A. f(1) = -13 and f(2) = 35; yes B. f(1) = -13 and f(2) = -35; no C. f(1) = 13 and f(2) = -35; yes D. f(1) = 13 and f(2) = 35; no
Graph the system of inequalities, and find the coordinates of the vertices.y - 3x ? 9,y + 3x ? -3,x ? 0,y ? 0
A.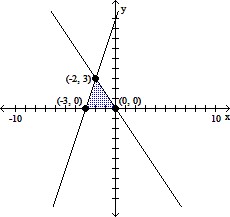 
B. 
C. 
D.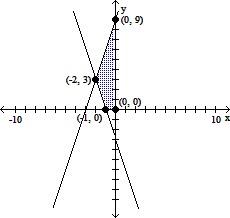 
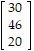
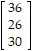
Solve the problem.The infant mortality rate at three different hospitals is given in the table below. Infant mortality rateHospital A0.008?Hospital B0.006Hospital C0.007The table below shows the number of live births at each of these hospitals in each of the years 1990-1992. Hospital A Hospital B Hospital C1990185024209701991121819607081992117621901075What matrix product displays the total number of infant deaths at the three hospitals in each of the years 1990-1992? Display the two matrices which must be multiplied and their product. Round numbers to the nearest whole number.
A.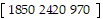 
= 
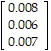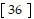
B. 
= 
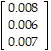C. 
= 
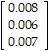D.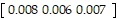 
= 