Solve the problem.A ship sailing parallel to shore sights a lighthouse at an angle of 15° from its direction of travel. After traveling 3 miles farther, the angle is 21°. At that time, how far is the ship from the lighthouse? If necessary, round to the nearest hundredth of a mile.
A. 7.43 mi
B. 2.17 mi
C. 3 mi
D. 10.29 mi
Answer: A
You might also like to view...
A truck must drop off furniture at 4 different homes (A, B, C, and D) as shown in the graph below, starting and ending at A. The numbers on the edges represent distances (in miles) between locations. The truck driver wants to minimize the total length of the trip.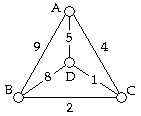 An optimal tour is given by:
An optimal tour is given by:
A. A, D, B, C, A. B. A, B, D, C, A. C. A, B, C, D, A. D. A, C, D, B, A. E. none of these
Using the pair of parametric equations, find the values of A and B in the table.x = 2t + 5, y = t - 3, for 0 ? t ? 7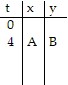
A. A = 7, B = -2 B. A = 8, B = 4 C. A = 2, B = -3 D. A = 13, B = 1
Solve the problem.A 9-ft. board is cut into 2 pieces so that one piece is 5 feet longer than 3 times the shorter piece. If the shorter piece is x feet long, find the lengths of both pieces.
A. shorter piece: 15 ft; longer piece: 32 ft. B. shorter piece: 1 ft.; longer piece: 8 ft. C. shorter piece: 4.5 ft; longer piece: 27 ft. D. shorter piece: 22 ft; longer piece: 27 ft.
Use the properties of logarithms to solve.log7 x + log7(x - 2) = log7 24
A. 7 B. 24 C. 6 D. 2