Use mathematical induction to prove that the statement is true for every positive integer n.0.32n < 0.32n-1
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, the left-hand side of the statement is 0.321 = 0.32. The right-hand side becomes 0.321-1 = 0.320 = 1. Since 0.32 < 1, the statement is true for n = 1.
b). Assume the statement is true for n = k:
0.32k < 0.32k-1
Multiply both sides by 0.32:
0.32 ? 0.32k = 0.32k+1 < 0.32 ? 0.32k-1 = 0.32k = 0.32(k+1)-1, or
0.32k+1 < 0.32(k+1)-1
Since the statement is true for n = k + 1 as long as it is true for n = k, and since the statement is true for n = 1, then it is true for all natural numbers n.
You might also like to view...
Solve the equation.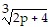 = 3
= 3
A. 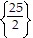
B. 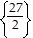
C. 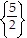
D. 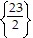
Find the LCD for the given fractions. and
and 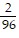
A. 336 B. 1344 C. 224 D. 672
Provide an appropriate response.Perform the indicated operation. Express as a power of 10. 
What will be an ideal response?
Factor out the GCF from the polynomial.10m8 + 6m6 - 20m4
A. 2m4(5m4 + 3m2 - 10) B. No common factor C. m4(10m4 + 6m2 - 20) D. 2(5m8 + 3m6 - 10m4)