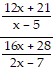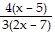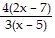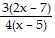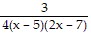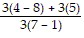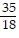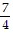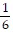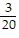Solve the problem.A manufacturer uses raw materials to produce p products each day. Suppose that each delivery of a particular material is $d, whereas the storage of that material is x dollars per unit stored per day. (One unit is the amount required to produce one product). How much should be delivered every x days to minimize the average daily cost in the production cycle between deliveries?

Question

What will be an ideal response?

Answer 1

If he asks for a delivery every x days, then he must order (px) to have enough material for that delivery cycle. The average amount in storage is approximately one-half of the delivery amount, or 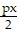. Thus, the cost of delivery and storage for each cycle is approximately
 Cost per cycle = delivery costs + storage costs
 Cost per cycle = d + 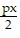 ? x
We compute the average daily cost c(x) by dividing the cost per cycle by the number of days x in the cycle.
 c(x) =  +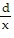 
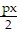
We find the critical points by determining where the derivative is equal to zero.
 c'(x) = - 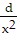 +  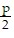= 0
 x = ±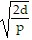 
Therefore, an absolute minimum occurs at 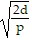 days.