Provide an appropriate response.The distribution of incomes tends to be skewed to the right because of outliers - a few extreme values lying far to the right of the bulk of the data (the few people with extremely large incomes). For the distribution of incomes in the U.S. which do you think will be larger, the mean or median? Which do you think is a more representative measure of center?
What will be an ideal response?
The mean will be larger. Explanations will vary. Possible answer: Since the mean takes into account the numerical value of every income, it is pulled in the direction of the extreme values, i.e. to the right. The mean is sensitive to outliers. For a skewed distribution the median is more representative of the bulk of the data as it is unaffected by the outliers.
You might also like to view...
Graph the pair of parametric equations with the aid of a graphing calculator.x = 3 cos t + cos 3t, y = 3 sin t - sin 3t, 0 ? t ? 2?
A.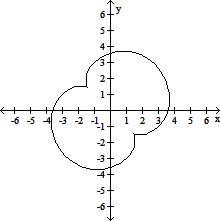 
B. 
C.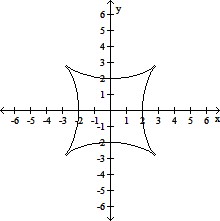 
D.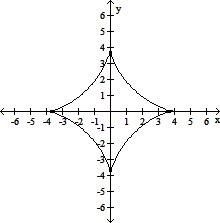 
Use slack variables to convert the constraints into linear equations.Maximizex + 2y + 3zsubject to:x + 4y + 8z ? 40 7x + y + 4z ? 50with:x ? 0, y ? 0, z ? 0
A. x + 4y + 8z = u - 40 7x + y +4z = v - 50 -x - 2y - 3z + M = 0 Maximize M given that x ? 0, y ? 0, z ? 0, u ? 0, v ? 0 B. x + 4y + 8z = u + 40 7x + y +4z = v + 50 -x - 2y - 3z = M Maximize M given that x ? 0, y ? 0, z ? 0, u ? 0, v ? 0 C. x + 4y + 8z + u = 40 7x + y + 4z + v = 50 -x - 2y - 3z + M = 0 Maximize M given that x ? 0, y ? 0, z ? 0, u ? 0, v ? 0 D. x + 4y + 8z + u = 40 7x + y + 4z + v = 50 x + 2y + 3z + M = 0 Maximize M given that x ? 0, y ? 0, z ? 0, u ? 0, v ? 0
Solve the problem.If f(x) = 
and g(x) =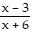 
, find (fg)(x).
A.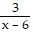 
B.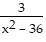 
C.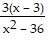 
D.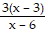 
Use the quadratic formula to find the roots of the equation. Find a decimal approximation to the nearest thousandth.x2 + 5x - 5 = 0
A. x = -11.708, x = 1.708 B. x = 5.854 C. x = -5.854 D. x = -5.854, x = 0.854