Solve the problem.Tides go up and down in a 13.2-hour period. The average depth of a certain river is 7 m and ranges from 3 to 11 m. The variation can be approximated by a sine curve. Write an equation of the form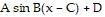
that gives the approximate variation y, if x is the number of hours after midnight and high tide occurs at 5:00 am.
A. y = 7 sin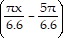 
B. y = 4 sin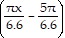 
C. y = 4 sin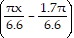 
D. y = 7 sin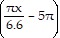 
Answer: C
You might also like to view...
Write a negation of the statement. Some photographs are not displayed at this exhibition.
A. All photographs are not displayed at this exhibition. B. No photographs are displayed at this exhibition. C. Some photographs are displayed at this exhibition. D. All photographs are displayed at this exhibition.
Find the area of the geometric figure.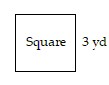
A. 7 sq yd B. 12 sq yd C. 6 sq yd D. 9 sq yd
At one high school, students can run the 100-yard dash in a mean of 15.2 seconds with a standard deviation of 0.9 seconds. The times are very closely approximated by a normal curve. Rounding to the nearest tenth of a percent as necessary, find the percent of times that are:Between 15.2 and 16.1 seconds
A. 34% B. 68% C. 13.5% D. 50%
A formula is given along with the values of all but one of the variables in the formula. Find the value of the variable not given.P = 2L + 2W; P = 18, W = 5
A. 9 B. 13 C. 4 D. 6.5