Write the number of rational and irrational zeros of the given cubic function.
?
x3 - 2
?
A. Rational zeros: 1; irrational zeros: 0
B. Rational zeros: 1; irrational zeros: 2
C. Rational zeros: 1; irrational zeros: 1
D. Rational zeros: 0; irrational zeros: 1
E. Rational zeros: 0; irrational zeros: 0
Answer: D
You might also like to view...
Evaluate the function for the given values of a and b. Then use the intermediate value theorem to determine which of the statements below is true.a = -1 and b = 0f(x) = 3x3 - 9x2 - 2x + 8
A. f(-1) and f(0) have the same sign, therefore the intermediate value theorem cannot be used to determine whether the function f has a real zero between -1 and 0. B. f(-1) and f(0) have opposite signs, therefore the function f does not have a real zero between -1 and 0. C. f(-1) and f(0) have the same sign, therefore the function f has a real zero between -1 and 0. D. f(-1) and f(0) have opposite signs, therefore the function f has a real zero between -1 and 0.
Solve the problem.This chart shows the fees for an 18 hole round of golf for each of the last 5 years at a local municipal golf course. Assume that this chart defines a function with the name of f. State the domain of f.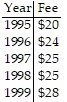
A. {(20, 1995), (24, 1996), (25, 1997), (25, 1998),(28, 1999)} B. {20, 24, 25, 28} C. {(1995, 20), (1996, 24), (1997, 25), (1998, 25),(1999, 28)} D. {1995, 1996, 1997, 1998, 1999}
Solve the equation symbolically.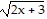 +
+ 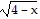 = 4
= 4
A. 3, 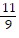
B. No solution
C. -3
D. 3
Evaluate the polynomial for the given value.-5x3 - 6x2 - x - 41; x = 0
A. -23 B. 0 C. -33 D. -41