Solve the problem.A company that produces handbags has found that revenue from the sales of the handbags is $8 per handbag, less sales costs of $50. Production costs are $75, plus $7 per handbag. Profit (P) is given by revenue (R) less cost (C), so the company must find the production level x that makes P > 0, that is, R - C > 0.(a) Write an expression for revenue, R, letting x represent the production level (number of handbags to be produced.)(b) Write an expression for production costs C in terms of x.(c) Write an expression for profit P, and then solve the inequality P > 0.(d) Describe the solution in terms of the problem.
A. (a) R = 8x - 50;
(b) C = 25 + 9x;
(c) P = (8x - 50) - (25 + 9x) = x - 75; x > 75;
(d) To make a profit, more than 75 handbags must be produced and sold.
B. (a) R = 8x - 50;
(b) C = 75 + 7x;
(c) P = (8x - 50) - (75 + 7x) = x - 125; x > 125;
(d) To make a profit, more than 125 handbags must be produced and sold.
C. (a) R = 8x - 50;
(b) C = 75 - 7x;
(c) P = (8x - 50) - (75 - 7x) = x - 75; x > 75;
(d) To make a profit, more than 75 handbags must be produced and sold.
D. (a) R = 8x + 50;
(b) C = 75 + 7x;
(c) P = (8x + 50) - (75 + 7x) = x - 25; x > 25;
(d) To make a profit, more than 25 handbags must be produced and sold.
Answer: B
You might also like to view...
Evaluate the integral.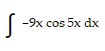
A. - 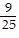 cos 5x -
cos 5x - 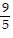 sin 5x + C
sin 5x + C
B. - 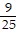 cos 5x -
cos 5x - 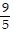 x sin 9x + C
x sin 9x + C
C. - 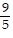 cos 5x - 9x sin 5x + C
cos 5x - 9x sin 5x + C
D. -  cos 5x -
cos 5x - 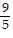 x sin 5x + C
x sin 5x + C
Solve the logarithmic equation.log x = 5
A. 5 B. 50 C. 100,000 D. 0.5
Use a calculator to find the value of the function in degrees. Round to the nearest hundredth when necessary.tan-1 0.4002
A. 113.59° B. 21.81° C. 23.59° D. -23.59°
Give the maximum number of zeros the polynomial function may have. Use Descarte's Rule of Signs to determine how many positive and how many negative zeros it may have.f(x) = 4x3 - 2x2 + x + 4
A. 3; 2 or 0 positive zeros; 2 or 0 negative zeros B. 3; 3 or 1 positive zeros; 3 or 1 negative zeros C. 3; 2 or 0 positive zeros; 1 negative zero D. 3; 2 or 0 positive zeros; 1 or 0 negative zeros