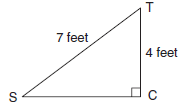
Use mathematical induction to prove the statement is true for all positive integers n.6n > 6n-1

Question

What will be an ideal response?

Answer 1

Answers may vary. Possible answer:
First, we show the statement is true when n = 1.
For n = 1, 61 > 61-1.
Since 61-1 = 60 = 1 and 61 > 1, P₁ is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
P_k: 6k > 6k-1  is assumed true.
On the basis of the assumption that P_k is true, we need to show that P_k+1 is true. 
P_k+1: 6k+1 > 6k
So we assume that 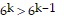 is true and multiply both sides of the equation by 6
6k? 6 > 6k-1? 6 
6k+1 > 6(k-1)+1
6k+1 > 6k
So P_k+1 is true if P_k is assumed true. Therefore, by the principle of mathematical induction, 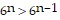 for all natural numbers n.