Solve and check.
+ 
= 
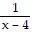A. x = 4
B. x = -1
C. x = -4
D. x = 1
Answer: D
You might also like to view...
Solve the problem.The line graph shows the cost of inflation. What cost $5000 in 1980 would cost the amount shown by the graph in subsequent years.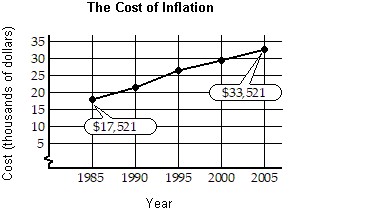 
Below are two mathematical models for the data shown in the graph. In each formula, C represents the cost x years after 1985 of what cost $5000 in 1980. Model 1: C = 798x + 17,521 Model 2: C = -x2 + 820x + 18,017(i) Use the graph to estimate the cost in 2000, to the nearest thousand dollars, of what cost $5000 in 1980.(ii) Use model 1 to determine the cost in 2000. How well does this describe your estimate from part (i)?(iii) Use model 2 to determine the cost in 2000. How well does this describe your estimate from part (i)?
A. (i) about $28,000; (ii) about $29,491, reasonably well; (iii) about $28,452, reasonably well B. (i) about $29,000; (ii) about $29,491, reasonably well; (iii) about $30,092, reasonably well C. (i) about $30,000; (ii) about $30,289, reasonably well; (iii) about $30,912, reasonably well D. (i) about $27,000; (ii) about $28,693, reasonably well; (iii) about $29,272, reasonably well
Arrange the polynomial in descending powers of the variable. Then find its degree and leading coefficient.-2 + 7x4 + 16x5
A. -2 + 7x4 + 16x5 , degree: 5, leading coefficient: -2 B. -2 + 7x4 + 16x5 , degree: 10, leading coefficient: -2 C. 16x5 + 7x4 - 2, degree: 9, leading coefficient: 16 D. 16x5 + 7x4 - 2, degree: 5, leading coefficient: 16
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. If necessary, round answers to two decimal places.f(x) = x4 - 5x3 + 3x2 + 9x - 3; (-5, 5)
A. local minimum at (-0.61, -5.64) local maximum at (1.41, 6.12) local minimum at (3, -3) B. local minimum at (-3, -3) local maximum at (-1.32, 5.64) local minimum at (0.57, -6.12) C. local minimum at (-0.57, -6.12) local maximum at (1.32, 5.64) local minimum at (3, -3) D. local minimum at (-1, -6) local maximum at (1, 6) local minimum at (3, -3)
Solve.On an expressway off-ramp, the road slopes downward five feet per 111 feet. Using a signed number, find the rate at which the road drops per foot.
A. - 
ft per foot
B. - 
ft per foot
C. -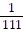 
ft per foot
D. - 5 ft per foot