Use mathematical induction to prove that the statement is true for every positive integer n.12 + 42 + 72 + . . . + (3n - 2)2 = 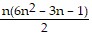
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 12 = 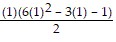 =
= 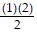 = 1. So, the statement is true for n = 1.
= 1. So, the statement is true for n = 1.
b). Assume the statement is true for n = k:
Sk = 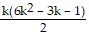 .
.
Also, if the statement is true for n = k + 1, then
Sk+1 = Sk + (3(k + 1) - 2)2 = 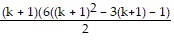 .
.
Subtract to get:
Sk+1 - Sk = (3(k + 1) - 2)2 = 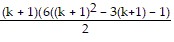 -
- 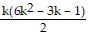
Expand both sides and collect like terms:
9k2 + 6k + 1 = 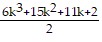 -
- 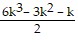
9k2 + 6k + 1 = 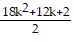 = 9k2 + 6k + 1
= 9k2 + 6k + 1
Since the equality holds, then the statement is true for n = k + 1 as long as it is true for n = k. Furthermore, the statement is true for n = 1. Therefore, the statement is true for all natural numbers n.
You might also like to view...
Determine how many components the graph has.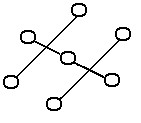
A. 3 B. 7 C. 5 D. 1
Perform the arithmetic.-2 + 15
A. -13 B. 17 C. 13 D. -17
Use the quadratic formula to solve the equation.x2 - 24x + 144 = 0
A. {12} B. {-12, 12} C. {-12} D. {-12 - i, -12 + i}
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator.logb (yz7)
A. 7 logb yz B. 7 logb y + 7 logb z C. logb y + 7 logb z D. logb y + logb7z