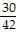Use mathematical induction to prove that the statement is true for every positive integer n.2n > n
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 31 = 3 > 1, so the statement is true for n = 1.
b). Assume that the statement is true for n = k:
3k > k
Multiply both sides by 3:
3?3k = 3k+1 > 3k
Also, since k ? 1, then 2k > 1, which can be re-written as 3k > k + 1. Thus,
3k+1 > k + 1
Since the statement is true for n = k + 1 as long as it is true for n = k, and since the statement is true for n = 1, then it is true for all natural numbers n.
You might also like to view...
Verify that the equation is an identity.cos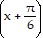 =
= 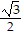 cos x -
cos x - 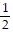 sin x
sin x
What will be an ideal response?
Solve the problem.What is 60% of 200?
A. 1.2 B. 120 C. 12 D. 1200
Solve the problem.A lake is stocked with 650 fish of a new variety. The size of the lake, the availability of food, and the number of other fish restrict growth in the lake to a limiting value of 4062. The population of fish in the lake after time t, in months, is given by the function, P(t) = 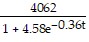 . After how many months will the population be 2312?
. After how many months will the population be 2312?
A. 7 B. 5 C. 12 D. 17
Write each fraction as an equivalent fraction with the LCD of the two fractions as the denominator.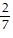 ,
, 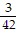 and
and 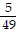
A. 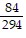 ;
; 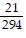 ;
; 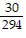
B. 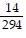 ;
; 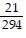 ;
; 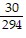
C. 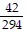 ;
; 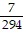 ;
; 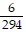
D.  ;
; 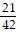 ;
;