Find the general solution for the differential equation. Then find the particular solution satisfying the initial condition.y' = 4x3; y(0) = -5
A. General solution: y = x4 + C; particular solution: y = x4 + 5
B. General solution: y = 4x4 + C; particular solution: y = 4x4 - 4
C. General solution: y = x4 + C; particular solution: y = x4 - 5
D. General solution: y = 4x3 + C; particular solution: y = 4x3 - 5
Answer: C
You might also like to view...
Find the derivative of the function.y = log |-9x|
A. 
B. 
C. - 
D. - 
Find the sum of the sequence.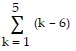
A. -15 B. -14 C. -1 D. -6
Evaluate the exponential expression.(-5)-2
A.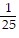 
B. 25
C. -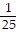 
D. -25
Solve the problem.An explosion causes debris to rise vertically with an initial velocity of 112 feet per second. The function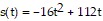 
describes the height of the debris above the ground, s(t), in feet, t seconds after the explosion. What is the instantaneous speed of the debris when it hits the ground?
A. 112 B. -224 C. -112 D. 224