Solve the problem.A person with no more than $3,000 to invest plans to place the money in two investments, telecommunications and pharmaceuticals. The telecommunications investment is to be no more than 4 times the pharmaceuticals investment. Write a system of inequalities to describe the situation. Let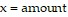 
to be invested in telecommunications and 
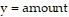to be invested in pharmaceuticals.
A. x + y = 3,000
y ? 4x
x ? 0
y ? 0
B. x + y ? 3,000
4x ? y
x ? 0
y ? 0
C. x + y ? 3,000
x ? 4y
x ? 0
y ? 0
D. x + y = 3,000
x ? 4y
x ? 0
y ? 0
Answer: C
You might also like to view...
Find the curvature of the curve r(t).r(t) = (2 + cos 10t - sin 10t)i + (2 + sin 10t + cos 10t)j + 2k
A. ? = 5
B. ? = 
C. ? = 
D. ? = 5
Factor.8z2 + 6z - 9
A. (8z + 1)(z - 9) B. (8z + 3)(z - 3) C. (2z - 3)(4z + 3) D. (2z + 3)(4z - 3)
Factor the trinomial completely, or state that the trinomial is prime.15x2 - 29x + 12
A. (3x + 4)(5x + 3) B. (3x - 4)(5x - 3) C. (15x + 4)(x + 3) D. prime
Solve the problem using the quadratic formula.When water runs out of a hole in a cylindrical container, the height of the water in the container can often be modeled by a quadratic function. Assume that the height of the water in a particular metal can with a small hole can be modeled by h(x) = 0.0005x2 - 0.17x + 8, where x is the time (sec) and h is the height (cm). Use the quadratic formula to estimate the earliest time when the height is 3 cm. Round your answer to the nearest second.
A. 40 sec B. 39 sec C. 33 sec D. 37 sec