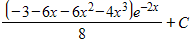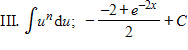Determine the most appropriate method or integral formula for evaluating the given integral. Next, evaluate the integral.
?
  I. Integration by parts

?

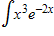
A. I. Integration by parts;  
B.
C.
D.
E. not integrable by any of the techniques we have studied

Answer: A

Mathematics

You might also like to view...

Find the probability.What is the probability that the arrow will land on an odd number?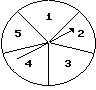

A. 1 
B.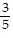
C.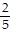
D. 0 

View
Mathematics

Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.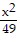 -  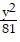= 1

A. center at (0, 0)
transverse axis is x-axis
vertices at (-9, 0) and (9, 0)  
foci at (- 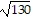, 0) and (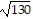, 0)
asymptotes of y = - 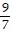 and y =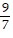 
B. center at (0, 0)
transverse axis is y-axis
vertices at (0, -7) and (0, 7)  
foci at (- 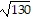, 0) and (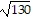, 0)
asymptotes of y = - 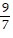 and y =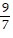 
C. center at (0, 0)
transverse axis is x-axis
vertices at (-7, 0) and (7, 0)  
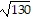foci at (- , 0) and (, 0)
asymptotes of y = - 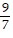 and y =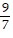 
D. center at (0, 0)
transverse axis is x-axis
vertices at (-7, 0) and (7, 0)  
foci at (-9, 0) and (9, 0)
asymptotes of y = - 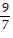 and y =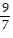 

View
Mathematics

For the rational function below (i) Find the intercepts for the graph; (ii) Determine the domain; (iii) Find any vertical or horizontal asymptotes for the graph; (iv) Sketch any asymptotes as dashed lines. Then sketch the graph of y = f(x).f(x) =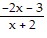 

A. (i) x intercept: - 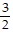; y intercept: -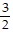 
(ii) Domain: all real numbers except -2
(iii) Vertical asymptote: x = -2; horizontal asymptote: y = -2
(iv)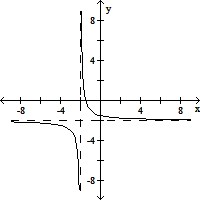

B. (i) x intercept: 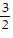; y intercept: -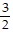 
(ii) Domain: all real numbers except 2
(iii) Vertical asymptote: x = 2; horizontal asymptote: y = -2
(iv)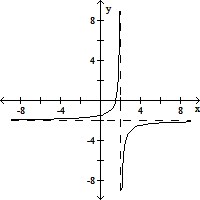

C. (i) x intercept: 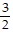; y intercept: -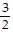 
(ii) Domain: all real numbers except 2
(iii) Vertical asymptote: x = 2; horizontal asymptote: y = -2
(iv)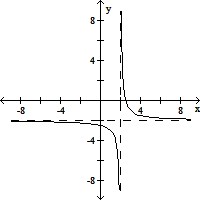

D. (i) x intercept: - 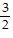; y intercept: -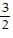 
(ii) Domain: all real numbers except -2
(iii) Vertical asymptote: x = -2; horizontal asymptote: y = -2
(iv)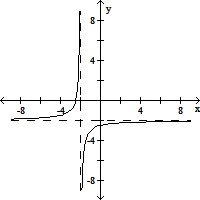

View
Mathematics

Solve the problem.The time of a telephone call (in minutes) to a certain town is a continuous random variable with a probability density function defined by 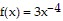 for 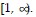 Find the probability: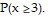 

A. 0.3066 B. 0.0759 C. 0.2402 D. 0.0370

View
Mathematics