Solve the problem.The 10 ft wall shown here stands 33 feet from the building. Find the length of the shortest straight beam that will reach to the side of the building from the ground outside the wall.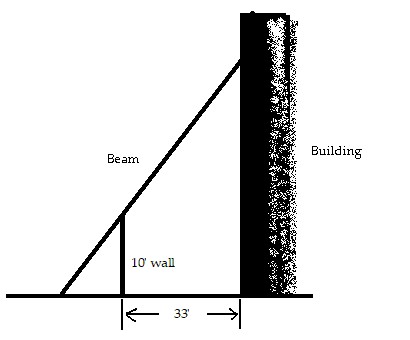
A. 43 ft
B. 56.7 ft
C. 58.7 ft
D. 57.7 ft
Answer: D
You might also like to view...
Solve the problem.A radio telescope has a parabolic surface. If it is 1 m deep and 20 m wide, how far is the focus from the vertex?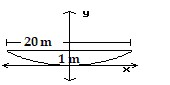 
A. 100 m B. 5 m C. 1 m D. 25 m
Solve the problem.Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 4.3 feet per second. Find a function, d(t), which gives the distance Ken is from the streetlight in terms of time. Find a function,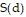 
, which gives the length of Ken's shadow in terms of d. Then find 
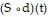. What is the meaning of 
?
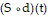A. (S ? d)(t) gives the distance Ken is from the streetlight in terms of time. B. (S ? d)(t) gives the time in terms of Ken's distance from the streetlight. C. (S ? d)(t) gives the length of Ken's shadow in terms of his distance from the streetlight. D. (S ? d)(t) gives the length of Ken's shadow in terms of time.
Multiply.3.1(-3.01)
A. 0.09 B. 6.11 C. 6.21 D. -9.331
Find the missing coefficient so that the lines are perpendicular.4x - y = 7 and y = Bx + 
A. B = 1
B. B = -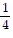 
C. B =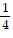 
D. B = 4