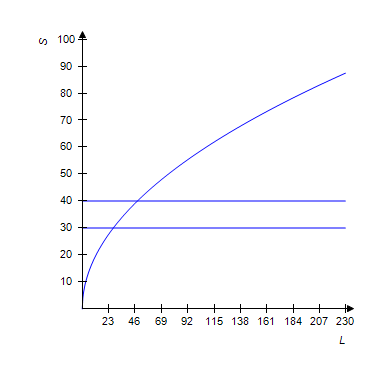
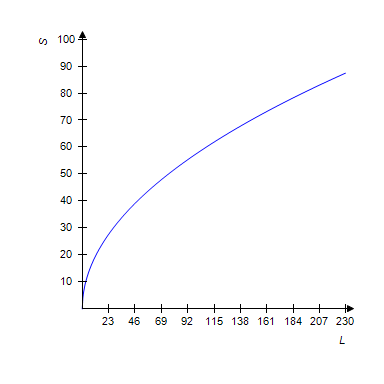
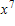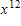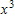When a car makes an emergency stop on dry pavement, it leaves skid marks on the pavement. The length L, in feet, of the skid marks is related to the speed S, in miles per hour, when the brakes were applied. The relationship is
.
A: Make a graph of S against L for skid mark lengths up to 200 feet.B: A man involved in an emergency stop claimed his speed was between 30 and 40 miles per hour. Add the horizontal lines represented by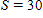
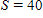
and 
to the graph you made in part A.C: What range of skid mark length would support the driver's claim? Round your answer to two decimal places/
What will be an ideal response?
?
?
B:
?
?
?
C: From 27.03 to 48.06 feet
You might also like to view...
Find the flux of the curl of field F through the shell S.F = exi + eyj + 3xyk; S is the portion of the paraboloid 1 - x2 - y2 = z that lies above the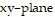 
A. -3 B. 3 C. -3? D. 0
Subtract. Simplify, if possible.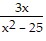
- 
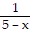
A.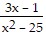 
B.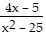 
C.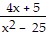 
D.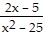 
Solve the problem.The cost C, in dollars, to produce graphing calculators is given by the function C(x) = 55x + 3500, where x is the number of calculators produced. How many calculators can be produced if the cost is limited to $119,000?
A. 1900 calculators B. 2227 calculators C. 2380 calculators D. 2100 calculators
Simplify the expression.
?
?
A. 
B. ?
C. ?
D. ?